Design a mealy machine for 2’s complement
Last Updated :
17 Oct, 2022
Mealy machine is a finite-state machine, its current state and the current inputs determines the output of this machine.
There is no final state in Mealy Machine .
Here we are going to design a Mealy Machine for 2’s Complement
Σ = { 0 , 1 }
2’s complement :
It is the mathematical operation on binary numbers. It is used for computation as a method of signed number representation. Its complement with respect to 2N defines the two’s complement an N-bit number.
Logic:-
First calculate 1’s complement of binary number, convert 1 to 0 and 0 to 1 and then add 1 to it. For example, if binary number is 1011 then its 1’s complement is 0100 and its 2’s complement is 0101
Design mealy machine :
- Take initial state A.
- If there are n number of zeros at initial state, it will remain at initial state.
- Whenever first input 1 is found then it gives output 1 and go to state B.
- After changing a condition we reverse the output .
- In state B, if input is zero, output will be 1. And if input is 1 then output will be 0.
The approach goes as follows:
- Start from right to left.
- Ignore all 0’s.
- When 1 comes ignore it and then take 1’s complement of every digit.
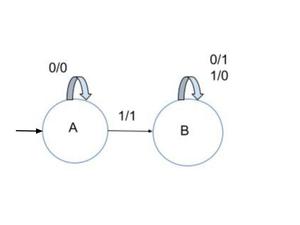
Mealy Machine for 2’s Complement
Figure – Mealy machine of 2’s complement
Example-1:
- Lets take 001 and we know that its 2’s complement is (110+1 = 111).
- So scan from right to left.
- On state A ‘1’ came first to go to stage B and in output write 1.
- On state B replace ‘0’ with ‘1’ and vice-versa.
- So finally we got 111 as output.
- Be aware that the output is also printed in right to left order.
Example-2:
- Lets take 01 and we know that its 2’s complement is (10+1 = 11).
- So scan from right to left.
- On state A ‘1’ came first to go to stage B and in output write 1.
- On state B replace ‘0’ with ‘1’ and vice-versa.
- So finally we got 11 as output.
- Be aware that the output is also printed in right to left order.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...