Derive the efficiency of Pure ALOHA protocol
Last Updated :
26 Apr, 2021
The efficiency of an ALOHA system is that fraction of all transmitted frames which escape collisions that is which do not get caught in collisions.
Consider ∞ number of interactive users at their computers (stations). Each user is either typing or waiting. Initially, all of them are in the typing state. When a user types a line, the user stops and waits. The station then transmits a frame containing this line and checks the channel to confirm the success. If it is successful then the user will start typing again, otherwise, the user waits and its frame is retransmitted much time till it is sent successfully.
Frame time :
Let the frame time be defined as the amount of time required to transmit the standard fixed length frame.
Note that Frame time = Frame length/Bit rate
We assume that ∞ number of users generates new frames according to Poisson’s distribution with an average N frame per frame time. The value of N > 1 indicates that the users are generating frames at a rate higher than that can be handled by the channel. So most of the frames will face collision.
Hence 0 <N <1 in order to reduce the number of collisions. Let there be k transmission attempts (including retransmissions) per frame time. The probability of k transmissions per frame time is also Poisson.
Let the mean number of transmissions be G per frame time. So, G≥N. At low load N ≈ 0 there will be fewer collisions so less number of retransmissions and G ≈ N. With the increase in load there are many collisions so G > N. Combining all these we can say that for all the loads the throughput is given by,
P0=S/G (Fraction of attempted frames that are transmitted successfully )
S = GP (throughput per frame time)
Where P’ = Probability that a frame does not suffer a collision.
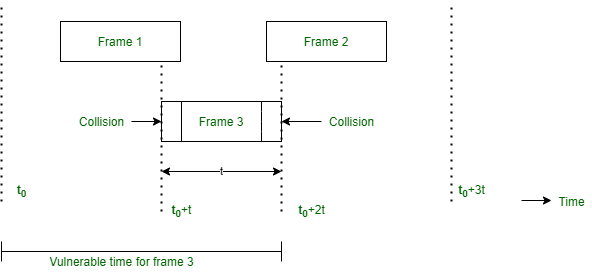
What is the condition for frame 3 in Fig. to arrive undamaged without collision?
Let t = time required to send a frame. If frame 1 is generated at any instant between t0 to (t0 + t) then it will collide with frame 3, Similarly, any frame 2 generated between (t0 + 1) and (t + 2t) also collides with frame 3. As per Poisson’s distribution, the Probability of Generating k frames during a given frame time is given by
P[k] = [ Gk x e(-G) ]/k! (Poisson’s distribution)
Where G = Number of stations willing to transmit data
So the probability of generating zero frames i.e. k= 0 is 3.
P[k]=[ G0 x e(-G) ]/0!
P[k]= e-2G
If an interval is two frame time long, the mean number of frames generated during that interval is 2G. The probability that another frame is transmitted during the Vulnerable period (the time when a collision can take place) is,
P0= e-2G
Fig. shows the relation between the offered traffic G and the throughput S. It shows that the maximum throughput occurs at G = 0.5
S= 0.5 x e-2 x 0.5
= 0.5 x e-1
= 0.184
= 18.4%
S(max) = 0.184. So the best possible channel utilization is 18.4%. It means 82% of frames end up in collisions and are therefore lost.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...