Derivative of the Sigmoid Function

Last Updated : 09 Jan, 2023

The sigmoid function is one of the most used activation functions in Machine learning and Deep learning. The sigmoid function can be used in the hidden layers, which take the output from the previous layer and brings the input values between 0 and 1. Now while working with neural networks it is necessary to calculate the derivate of the activation function.

The formula of the sigmoid activation function is:

$\begin{aligned}F(x) &= \sigma(x)\\ &= \frac{1}{1+e^{-x}}\end{aligned}$

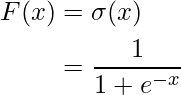
The graph of the sigmoid function looks like an S curve, where the function of the sigmoid function is continuous and differential at any point in its area.

The sigmoid function is also known as the squashing function, as it takes the input from the previously hidden layer and squeezes it between 0 and 1. So a value fed to the sigmoid function will always return a value between 0 and 1, no matter how big or small the value is fed.

Why Sigmoid Activation function is squeezing function?

As the activation function squeezes the input values fed to the hidden layers, the function returns the output between 0 and 1 only. So no matter how positive or negative numbers are fed to the layer, this function squeezes it between 0 and 1.

What is the main issue with the sigmoid function while backpropagation?

The main issue related to the activation function is when the new weights and biases are calculated by the gradient descent algorithm, if these values are very small, then the updates of the weights and biases will also be very low and hence, which results in vanishing gradient problem, where the model will not learn anything.

Graphically, the sigmoid function looks as shown below which is similar to S but rotated 90 degrees anti-clockwise.

Sigmoid function graph

Applications of Sigmoid Function

If we are using a linear activation function in the neural network then the model will only be able to separate the data linearly. Resulting a bad behavior on the nonlinear data. But if we add one more hidden layer with the sigmoid activation function then the model will also be able to perform better on a non-linear dataset and hence the performance of the model increases with non-linear data.

Now while performing the backpropagation algorithm on the neural network, the model calculated and updates the weights and biases of the neural network, this updation will happen by calculating the derivative of the activation function. Since the derivative of the sigmoid function is very easy as it is the only function that appears in its derivative itself. Also, the sigmoid function is differentiable on any point, hence it helps calculate better perform the backpropagation algorithm in the neural network.

Step 1: Differentiating both sides with respect to x.

$\begin{aligned} F^{'}(x) &= \frac{d}{dx}\left(\frac{1}{1+e^{-x} }\right )\\ \end{aligned}$

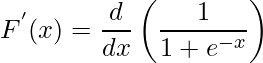
Step 2: Apply the reciprocating/chain rule.

$\begin{aligned} F^{'}(x) &= \frac{d}{dx}\left(\frac{1}{1+e^{-x} }\right )\\ &= -\frac{1}{\left(1+e^{-x} \right )^2}\frac{d}{dx}\left(1+e^{-x} \right )\\ &= -\frac{1}{\left(1+e^{-x} \right )^2}\cdot e^{-x}\frac{d}{dx}\left(-x \right )\\ &= \frac{e^{-x}}{\left(1+e^{-x} \right )^2} \end{aligned}$

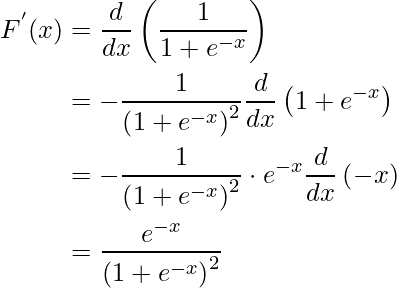
Step 3: Modify the equation for a more generalized form.

$\begin{aligned} \sigma^{'}(x) &= \frac{e^{-x}}{\left(1+e^{-x} \right )^2}\\ &= \frac{1+e^{-x}-1}{\left(1+e^{-x} \right )^2}\\ &= \frac{1}{1+e^{-x} }-\frac{1}{\left(1+e^{-x} \right )^2}\\ &= \frac{1}{\left(1+e^{-x} \right )}\cdot \left(1 -\frac{1}{1+e^{-x}}\right )\\ &= \sigma(x) \left(1 -\sigma(x)\right ) \end{aligned}$

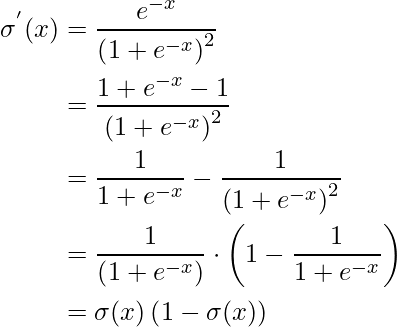
The above equation is known as the generalized form of the derivation of the sigmoid function. The below image shows the derivative of the sigmoid function graphically.