A spherical mirror or a mirror that is a part of a sphere is a mirror that has the shape of a piece that is cut out of a spherical surface or material. There are two types of spherical mirrors that are the concave and convex mirror. The curved surface we see of a shining or a shiny spoon can be considered as a curved mirror. The most widely and commonly used type of curved mirror is spherical mirrors. The reflecting surface of such mirrors is considered to form a part of the surface of any sphere. Those mirrors which possess reflecting surfaces which are spherical are called spherical mirrors.
Basic Terms for Spherical Mirrors
There are some common terms that we need to know while studying spherical mirrors, and they are as follows:
- Centre of Curvature: It is represented by the capital letter C. The point which is in the centre of the mirror surface passes through the curve of the mirror and has the same tangent and curvature at that point.
- Radius of Curvature: It is represented by the capital letter R. Radius of curvature is twice the focal length, R = 2f. It is considered as the linear distance between the pole and the centre of curvature.
- Principal axis: An imaginary line that passes through the optical centre and from the centre of curvature of a spherical mirror.
- Pole: The midpoint or the centre point of the spherical mirror. It is represented by capital P. All the measurements are made from it only.
- Aperture: An aperture of a mirror is a point from which the reflection of light actually takes place or happens. It also gives an idea about the size of the mirror.
- Principal Focus: Principal Focus can be called the Focal Point also. It is present on the axis of a mirror where the rays of light parallel to the principal axis converge or appear to converge or diverge after reflection.
- Focus: It is any given point on the principal axis where light rays parallel to the principal axis will converge or appear to converge after getting reflected from the mirror.
Mirror Formula
To do the sums related to the spherical mirrors, the formula used is known as the mirror formula. It is used to calculate the focal length, image distance, object distance, and also the magnification or any other thing required. We usually put the formula first and then put the signs so as to do the sums to minimize any error which can be generated. The sign conventions which are to be followed while using the mirror formula are fixed so from the above-given diagram we can easily put the signs according to the requirement to get the required result.
Usually, if the object is located on the left side of the principal axis from the mirror then the object distance is taken negative. While if it is located on the right side it is taken to be positive. The sign of focal length depends on the type of mirror we are using, as for the concave mirror it is negative and for the convex mirror on the other hand is positive always. It is to be mentioned again that we have to follow the sign conventions strictly to get the correct answer.
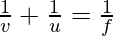
Where u = object distance
v = image distance
f = focal length of mirror
Derivation of the Mirror Formula
The derivation of the mirror formula or spherical mirror formula is one of the most common formulas in optics. The mirror formula can be termed as the formula in which the relationship between the distance of object represented as ‘u’ and the distance of the image represented as ‘v’, and the focal length of the mirror given as ‘f’. The formula is applicable for both, plane mirrors as well as for spherical mirrors including convex and concave mirror both. The mirror formula is given as:
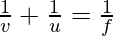
Assumptions which are made for the Derivation of the Mirror Formula:
The following considerations are taken in order to get the mirror formula derived:
- The object and image distance are being measured from the pole of the mirror.
- According to the sign convention, the negative sign indicates all the distances which are measured in the direction opposite to the incident ray whereas the positive sign indicates all the distances which are measured in the direction of the incident ray.
- The distance below the axis is taken to be negative whereas the distance above is taken to be positive.
Consider the diagram given below:

From the figure above, the object AB is placed at a distance of U from P which is known as the pole of the mirror. From the diagram given we can also say that the image A1B1 is formed at V from the mirror.
Now from the diagram, it is clear that according to the law of vertically opposite angles that the opposite angles are equal to each other. So it can be written as the:
∠ACB = ∠A1CB1
Similarly
∠ABC = ∠A1B1C(RIGHT ANGLES)
Now since two angles of triangles ACB and A1CB1 are equal and therefore the third angle is also equal and is given by,
∠ BAC = ∠ B1A1C, and
AB/A1B1 = BC/B1C ……..(1)
Similarly, the triangle of FED and FA1B1 are also equal and similar hence
ED/A1B1 = EF/FB1
Also since ED is equal to AB, so we have,
AB/A1B1 = EF/FB1 ………(2)
Combining 1 and 2 we get
BC/B1C = EF/FB1
Consider the point D is very close to P and so EF= PF, therefore
BC/B1C = PF/FB1
From the above diagram BC = PC – PB and B1C = PB1 – PC and FB1 = PB1 – PF
(0PC- PB)/(PB1-PC) = (PF)/(PB1-PF)
Now substituting the values of above segments along with the sign given we have,
PC = -R
PB = u
PB1 = -v
PF = -f
So the above equation now becomes,
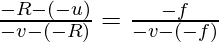
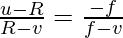
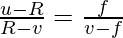
Solving it we have,
uv- uf – Rv + Rf = Rf – vf
uv – uf – Rv + vf = 0
As R = 2f (radius of curvature is twice that of focal length), therefore
uv – uf – 2fv + vf = 0
uv – uf – vf = 0
Solving it further and also dividing with “uv” we get,
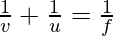
which is the required mirror formula.
Sign Convention for Spherical Mirror
Usually, if the object is located on the left side of the principal axis from the mirror then the object distance is taken negative. While if it is located on the right side it is taken to be positive. The sign of focal length depends on the type of the mirror we are using, as for the concave mirror it is negative and for the convex mirror on the other hand is positive always. It is to be mentioned again that we have to follow the sign conventions strictly to get the correct answer. Heights which are above the principal axis are positive and below are negative.

Sample Problems
Question 1: What is the image distance in case of concave mirror if the object distance is 4 cm? It is given that the focal length of the mirror is 2 cm.
Solution:
As we know from mirror formula,
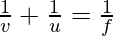
Where u= object distance= -4cm
v= image distance=?
f= focal length of mirror= -2cm
Putting values we get
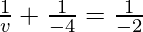
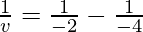
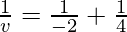
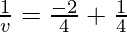
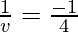
v = -4 cm
Hence, the object is located 4cm in front of the mirror.
Question 2: What is the image distance in case of convex mirror if the object distance is 12 cm? It is given that the focal length of the mirror is 12 cm.
Solution:
As we know from mirror formula,
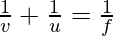
Where u= object distance= -12cm
v= image distance=?
f= focal length of mirror= 12cm
Putting values we get
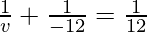
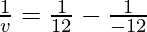
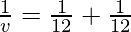
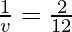
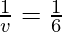
v = 6 cm
Hence, the image is located 6cm behind the mirror.
Question 3: What is the image distance in case of concave mirror if the object distance is 30 cm? It is given that the focal length of the mirror is 30 cm.
Solution:
As we know from mirror formula,
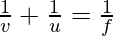
Where u= object distance= -30cm
v = image distance=?
f = focal length of mirror= -30cm
Putting values we get
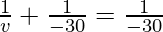
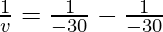
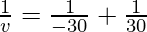
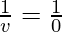

Therefore, v= infinity
Hence, the image will be formed at infinity.
Question 4: Find out the focal length with sign in case of concave mirror with a radius of curvature 20 cm.
Solution:
As we know that R = 2f
Where R= radius of curvature of concave mirror, f= focal length of concave mirror
R= 2f
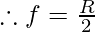
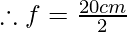
f= -10cm (negative indicates that it is a concave mirror.)
Hence, the focal length of the concave mirror is 10 cm.
Question 5: What is the image distance in case of concave mirror if the object distance is 16 cm? It is given that the focal length of the mirror is 8 cm.
Solution:
As we know from mirror formula,
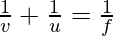
Where u= object distance= -16cm
v= image distance=?
f= focal length of mirror= -8cm
Putting values we get
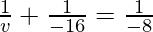
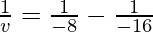

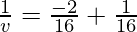
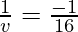
v= -16 cm
Hence the object is located 16 cm in front of the mirror.
Question 6: What is the image distance in case of convex mirror if the object distance is 16 cm? It is given that the focal length of the mirror is 16 cm.
Solution:
As we know from mirror formula,
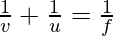
Where u= object distance= -16cm
v= image distance=?
f= focal length of mirror= +16cm
Putting values we get
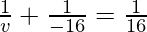
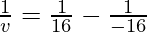
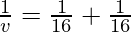
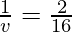

v= 8 cm
Hence, the image is located 8 cm behind the mirror.
Share your thoughts in the comments
Please Login to comment...