Delete Text in Microsoft Word
Last Updated :
06 Jun, 2021
MS-Word is a word processing application, and it is a very interactive and user-friendly tool. We use MS-Word for editing the already existing document and also for creating new documents. It is easy to use and learn. It is also very popular because of the vast features and tools provided by it to its user.
Deleting the Text
It is also one of the many features which are there in MS-Word. This feature is used when we make mistake while typing and want to delete it or want to delete some text or paragraph which is no more required.
We can do this particular operation with the Backspace key or Delete key which is present on the keyboard.
Let us now see how to delete the text step by step with help of images and instructions. This operation is Basic and easy to learn.
Method 1. Deleting the text with the help of Backspace key
We can delete any word by simply using the Backspace key repeatedly, but when the text is a bit long like a whole paragraph then it is very much time taking. So for that, we will see below how to do it.
Steps to follow:
Step 1: First open MS-Word on your PC.
Step 2: Now, Open the document or create a new one in which you want to perform this operation.
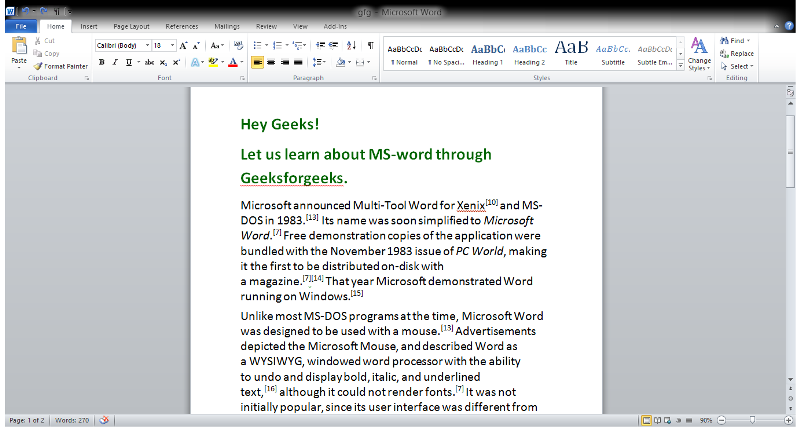
Step 3: Now, Select the Text which you want to delete.
Step 4: Now, Press the “Backspace” key to delete the selected text.
Step 5: So, the text is deleted successfully.

Method 2. Deleting the text with help of Delete key
Steps to follow:
Step 1: First open MS-Word on your PC.
Step 2: Now, Open the document or create a new one in which you want to perform this operation.

Step 3: Now, Select the Text which you want to delete.
Step 4: Now, Press the “Delete” key to delete the selected text.
Step 5: So, the text is deleted successfully.

So, this is a very basic operation and easy to learn.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...