Definite Integral | Mathematics
Last Updated :
29 Nov, 2022
Definite integrals are the extension after indefinite integrals, definite integrals have limits [a, b]. It gives the area of a curve bounded between given limits. 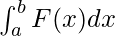 , It denotes the area of curve F(x) bounded between a and b, where a is the lower limit and b is the upper limit.
, It denotes the area of curve F(x) bounded between a and b, where a is the lower limit and b is the upper limit.
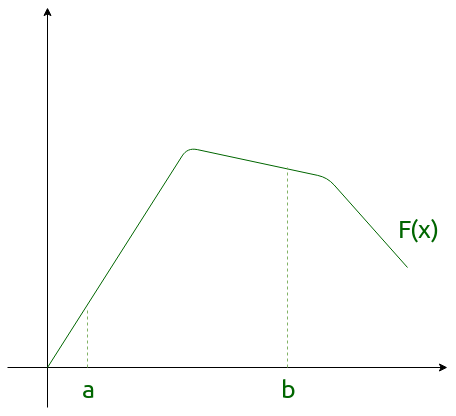
Note: If f is a continuous function defined on the closed interval [a, b] and F be an anti derivative of f.
Then ![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx= \left [ F(x) \right ]_{a}^{b}\right = F(b)-F(a)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-75e952f5725e5b873cbea81f3e509f0e_l3.png) Here, the function f needs to be well defined and continuous in [a, b].
Here, the function f needs to be well defined and continuous in [a, b].
Example: 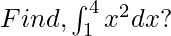 Solution:
Solution: ![Rendered by QuickLaTeX.com Since, \int x^{2}=\frac{x^{3}}{3} \newline \newline \textup{Then F(x)} =\frac{x^{3}}{3} \newline \newline [F(x)]_{1}^{4}= F(4)-F(1) \newline \newline =[\frac{4^{3}}{3} - \frac{1^{3}}{3}]=\frac{65}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-97f875dacf7c94e71ae2fd05ca508ee9_l3.png)
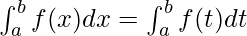
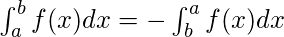
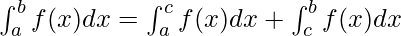
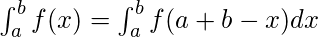
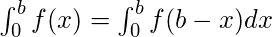
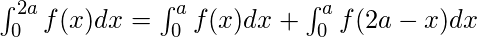
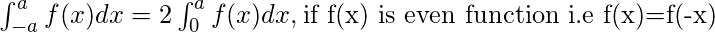
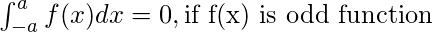
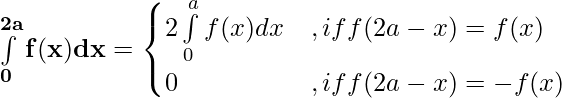
These properties can be used directly to find the value of a particular definite integral and also interchange to other forms if required.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...