Deep Q-Learning

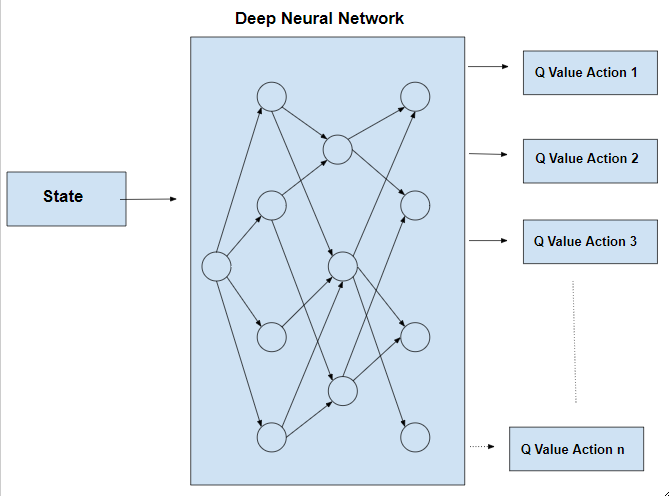
Q-Learning is required as a pre-requisite as it is a process of Q-Learning creates an exact matrix for the working agent which it can “refer to” to maximize its reward in the long run. Although this approach is not wrong in itself, this is only practical for very small environments and quickly loses it’s feasibility when the number of states and actions in the environment increases. The solution for the above problem comes from the realization that the values in the matrix only have relative importance ie the values only have importance with respect to the other values. Thus, this thinking leads us to Deep Q-Learning which uses a deep neural network to approximate the values. This approximation of values does not hurt as long as the relative importance is preserved. The basic working step for Deep Q-Learning is that the initial state is fed into the neural network and it returns the Q-value of all possible actions as an output. The difference between Q-Learning and Deep Q-Learning can be illustrated as follows:

Pseudo Code:

Initialize 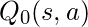 for all pairs (s,a)s = initial statek = 0while(convergence is not achieved){    simulate action a and reach state s'    if(s' is a terminal state)    {        target = R(s,a,s')    }    else    {        target = R(s,a,s') +     }        s = s'}

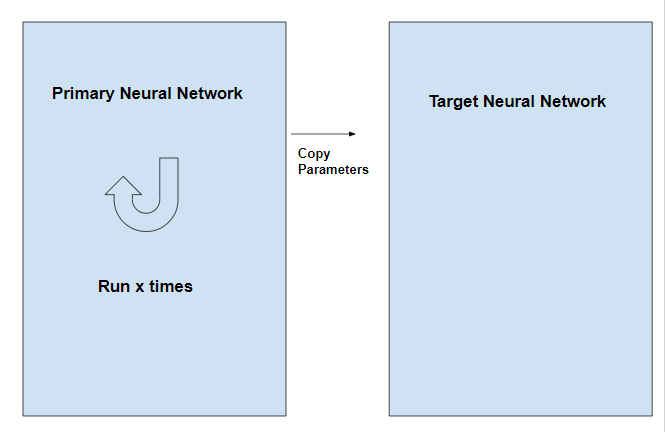
Observe that in the equation target = R(s,a,s’) + , the term is a variable term. Therefore in this process, the target for the neural network is variable unlike other typical Deep Learning processes where the target is stationary. This problem is overcome by having two neural networks instead of one. One neural network is used to adjust the parameters of the network and the other is used for computing the target and which has the same architecture as the first network but has frozen parameters. After an x number of iterations in the primary network, the parameters are copied to the target network.

Deep Q-Learning is a type of reinforcement learning algorithm that uses a deep neural network to approximate the Q-function, which is used to determine the optimal action to take in a given state. The Q-function represents the expected cumulative reward of taking a certain action in a certain state and following a certain policy. In Q-Learning, the Q-function is updated iteratively as the agent interacts with the environment. Deep Q-Learning is used in various applications such as game playing, robotics and autonomous vehicles.

Deep Q-Learning is a variant of Q-Learning that uses a deep neural network to represent the Q-function, rather than a simple table of values. This allows the algorithm to handle environments with a large number of states and actions, as well as to learn from high-dimensional inputs such as images or sensor data.

One of the key challenges in implementing Deep Q-Learning is that the Q-function is typically non-linear and can have many local minima. This can make it difficult for the neural network to converge to the correct Q-function. To address this, several techniques have been proposed, such as experience replay and target networks.

Experience replay is a technique where the agent stores a subset of its experiences (state, action, reward, next state) in a memory buffer and samples from this buffer to update the Q-function. This helps to decorrelate the data and make the learning process more stable. Target networks, on the other hand, are used to stabilize the Q-function updates. In this technique, a separate network is used to compute the target Q-values, which are then used to update the Q-function network.

Deep Q-Learning has been applied to a wide range of problems, including game playing, robotics, and autonomous vehicles. For example, it has been used to train agents that can play games such as Atari and Go, and to control robots for tasks such as grasping and navigation.