Decimal Number System
Last Updated :
16 Apr, 2020
A number system can be considered as a mathematical notation of numbers using a set of digits or symbols. In simpler words the number system is a method of representing numbers. Every number system is identified with the help of its base or radix. For example, Binary, Octal, Decimal and Hexadecimal Number systems are used in microprocessor programming.
Decimal Number System :
If the Base value of a number system is 10. This is also known as base-10 number system which has 10 symbols, these are: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Position of every digit has a weight which is a power of 10.
then it is called the Decimal number system which has the most important role in the development of science and technology. This is the weighted (or positional) number representation, where value of each digit is determined by its position (or their weight) in a number.
Each position in the decimal system is 10 times more significant than the previous position, that means the numeric value of a decimal number is determined by multiplying each digit of the number by the value of the position in which the digit appears and then adding the products.
Example-1: The number 2020 is interpreted as:-
= (2020)10
= (1024 + 512 + 256 + 128 + 64 + 32 + 4)10
= (210x1+29x1+28x1+27x1+26x1+25x1+24x0+23x0+22x1+21x0+20x0)10
= (11111100100)2

Therefore,
= (2020)10 = (11111100100)2
Example-2: The number 2020.50 is interpreted as:-
= (2020.50)10
= (1024 + 512 + 256 + 128 + 64 + 32 + 4 + (1/2))10
= (210x1+29x1+28x1+27x1+26x1+25x1+24x0+23x0+22x1+21x0+20x0+2-1x1)10
= (11111100100.1)2
Therefore,
= (2020.50)10 = (11111100100.1)2
Note :
Right most bit is the least significant bit (LSB) and left most bit is the most significant bit (MSB).
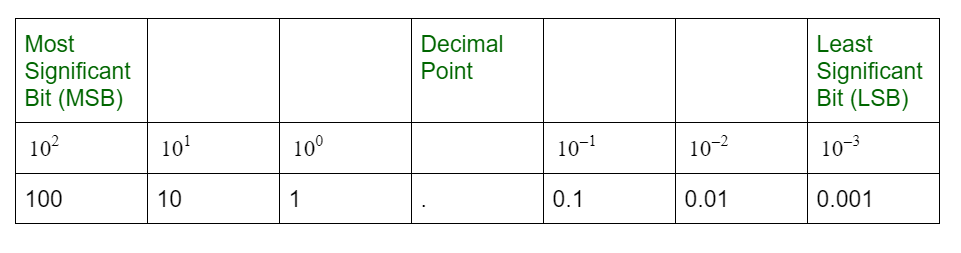
In general, a number expressed in the base-r system has coefficients multiplied by power of r. The coefficient aj ranges from 0 to (r-1). Representing real number in base-r is as following below:

Where, a0, a1, … a(n-1) and an are integer part digits, n is the total number of integer digits.
a-1, a-2, … and a-m are fractional part digits, m is the total number of fractional digits.
Advantages and disadvantages of Decimal Number System :
- Advantages – easy readability, used by humans, and easy to manipulate.
- Disadvantages – wastage of space and time.
9’s and 10’s Complement of Decimal (Base-10) Number :
- Simply, 9’s Complement of a decimal number is the subtraction of it’s each digits from 9. For example, 9’s complement of decimal number 2005 is 9999 – 2005 = 7994.
- 10’s Complement of decimal number is 9’s complement of given number plus 1 to the least significant bit (LSB). For example 10’s complement of decimal number 2005 is (9999 – 2005) + 1 = 7995.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...