Deadlock Detection Algorithm in Operating System
Last Updated :
12 Feb, 2024
Deadlock Avoidance Algorithm/ Bankers Algorithm:
What is a deadlock detection algorithm in operating systems?
A deadlock detection algorithm is a technique used by an operating system to identify deadlocks in the system. This algorithm checks the status of processes and resources to determine whether any deadlock has occurred and takes appropriate actions to recover from the deadlock.
The algorithm employs several times varying data structures:
- Available –
A vector of length m indicates the number of available resources of each type.
- Allocation –
An n*m matrix defines the number of resources of each type currently allocated to a process. The column represents resource and rows represent a process.
- Request –
An n*m matrix indicates the current request of each process. If request[i][j] equals k then process Pi is requesting k more instances of resource type Rj.
This algorithm has already been discussed here
Now, the Bankers algorithm includes a Safety Algorithm / Deadlock Detection Algorithm
The algorithm for finding out whether a system is in a safe state can be described as follows:
Steps of Algorithm:
- Let Work and Finish be vectors of length m and n respectively. Initialize Work= Available. For i=0, 1, …., n-1, if Requesti = 0, then Finish[i] = true; otherwise, Finish[i]= false.
- Find an index i such that both
a) Finish[i] == false
b) Requesti <= Work
If no such i exists go to step 4.
- Work= Work+ Allocationi
Finish[i]= true
Go to Step 2.
- If Finish[i]== false for some i, 0<=i<n, then the system is in a deadlocked state. Moreover, if Finish[i]==false the process Pi is deadlocked.
For example,
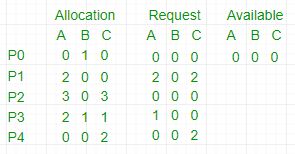
- In this, Work = [0, 0, 0] &
Finish = [false, false, false, false, false]
- i=0 is selected as both Finish[0] = false and [0, 0, 0]<=[0, 0, 0].
- Work =[0, 0, 0]+[0, 1, 0] =>[0, 1, 0] &
Finish = [true, false, false, false, false].
- i=2 is selected as both Finish[2] = false and [0, 0, 0]<=[0, 1, 0].
- Work =[0, 1, 0]+[3, 0, 3] =>[3, 1, 3] &
Finish = [true, false, true, false, false].
- i=1 is selected as both Finish[1] = false and [2, 0, 2]<=[3, 1, 3].
- Work =[3, 1, 3]+[2, 0, 0] =>[5, 1, 3] &
Finish = [true, true, true, false, false].
- i=3 is selected as both Finish[3] = false and [1, 0, 0]<=[5, 1, 3].
- Work =[5, 1, 3]+[2, 1, 1] =>[7, 2, 4] &
Finish = [true, true, true, true, false].
- i=4 is selected as both Finish[4] = false and [0, 0, 2]<=[7, 2, 4].
- Work =[7, 2, 4]+[0, 0, 2] =>[7, 2, 6] &
Finish = [true, true, true, true, true].
- Since Finish is a vector of all true it means there is no deadlock in this example.
There are several algorithms for detecting deadlocks in an operating system, including:
- Wait-For Graph: A graphical representation of the system’s processes and resources. A directed edge is created from a process to a resource if the process is waiting for that resource. A cycle in the graph indicates a deadlock.
- Banker’s Algorithm: A resource allocation algorithm that ensures that the system is always in a safe state, where deadlocks cannot occur.
- Resource Allocation Graph: A graphical representation of processes and resources, where a directed edge from a process to a resource means that the process is currently holding that resource. Deadlocks can be detected by looking for cycles in the graph.
- Detection by System Modeling: A mathematical model of the system is created, and deadlocks can be detected by finding a state in the model where no process can continue to make progress.
- Timestamping: Each process is assigned a timestamp, and the system checks to see if any process is waiting for a resource that is held by a process with a lower timestamp.
These algorithms are used in different operating systems and systems with different resource allocation and synchronization requirements. The choice of algorithm depends on the specific requirements of the system and the trade-offs between performance, complexity, and accuracy.
If a system does not employ either a deadlock prevention or deadlock avoidance algorithm then a deadlock situation may occur. In this case-
- Apply an algorithm to examine the system’s state to determine whether deadlock has occurred.
- Apply an algorithm to recover from the deadlock. For more refer- Deadlock Recovery
Advantages of Deadlock Detection Algorithms in Operating Systems:
- Improved System Stability: Deadlocks are a major concern in operating systems, and detecting and resolving deadlocks can help to improve the stability of the system.
- Better Resource Utilization: By detecting deadlocks and freeing resources, the operating system can ensure that resources are efficiently utilized and that the system remains responsive to user requests.
- Easy Implementation: Some deadlock detection algorithms, such as the Wait-For Graph, are relatively simple to implement and can be used in a wide range of operating systems and systems with different resource allocation and synchronization requirements.
Disadvantages of Deadlock Detection Algorithms in Operating Systems:
- Performance Overhead: Deadlock detection algorithms can introduce a significant overhead in terms of performance, as the system must regularly check for deadlocks and take appropriate action.
- Complexity: Some deadlock detection algorithms, such as the Resource Allocation Graph or Timestamping, are more complex to implement and require a deeper understanding of the system and its behavior.
- False Positives and Negatives: Deadlock detection algorithms are not perfect and may produce false positives or negatives, indicating the presence of deadlocks when they do not exist or failing to detect deadlocks that do exist.
- Overall, the choice of deadlock detection algorithm depends on the specific requirements of the system, the trade-offs between performance, complexity, and accuracy, and the risk tolerance of the system. The operating system must balance these factors to ensure that deadlocks are detected and resolved effectively and efficiently.
FAQ:
How does a deadlock detection algorithm work?
A deadlock detection algorithm works by analyzing the status of processes and resources in the system. It identifies any circular dependency between the processes and resources and determines whether a deadlock has occurred. If a deadlock is detected, the algorithm takes appropriate actions to recover from the deadlock.
What are the advantages of using a deadlock detection algorithm in operating systems?
The advantages of using a deadlock detection algorithm in operating systems include improved system stability, better resource utilization, and easy implementation.
What are the disadvantages of using a deadlock detection algorithm in operating systems?
The main disadvantage of using a deadlock detection algorithm is the performance overhead it may impose on the system. Additionally, the algorithm may require complex implementation, and the recovery from deadlock may take some time.
What are some common deadlock detection algorithms used in operating systems?
Some common deadlock detection algorithms used in operating systems include the Wait-For Graph algorithm, the Banker’s algorithm, the Resource Allocation Graph algorithm, and the Detection by System Modeling algorithm.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...