Database Design(Normal Forms)
Question 1
For the relation R(ABCDEFGH) with FD's= {CH->G, A->BC, B->CHF, E->A, F->EG such that F+ is exactly the set of FDs that hold for R.} Consider the FDs given in above question. The relation R is
Question 3
Consider a relational table with a single record for each registered student with the following attributes.
1. Registration_Num: Unique registration number of each registered student 2. UID: Unique identity number, unique at the national level for each citizen 3. BankAccount_Num: Unique account number at the bank. A student can have multiple accounts or join accounts. This attribute stores the primary account number. 4. Name: Name of the student 5. Hostel_Room: Room number of the hostelWhich one of the following option is INCORRECT?
Question 4
Consider the following relational schema:
Suppliers(sid:integer, sname:string, city:string, street:string) Parts(pid:integer, pname:string, color:string) Catalog(sid:integer, pid:integer, cost:real)Assume that, in the suppliers relation above, each supplier and each street within a city has a unique name, and (sname, city) forms a candidate key. No other functional dependencies are implied other than those implied by primary and candidate keys. Which one of the following is TRUE about the above schema?
Question 5
Consider the following relational schemes for a library database:
Book (Title, Author, Catalog_no, Publisher, Year, Price)
Collection (Title, Author, Catalog_no)
with in the following functional dependencies:
I. Title Author --> Catalog_no II. Catalog_no --> Title, Author, Publisher, Year III. Publisher Title Year --> PriceAssume {Author, Title} is the key for both schemes. Which of the following statements is true?
Question 6
Consider the relation scheme R = {E, F, G, H, I, J, K, L, M, N} and the set of functional dependencies {{E, F} -> {G}, {F} -> {I, J}, {E, H} -> {K, L}, K -> {M}, L -> {N} on R. What is the key for R?
Question 7
Given the following two statements:
S1: Every table with two single-valued
attributes is in 1NF, 2NF, 3NF and BCNF.
S2: AB->C, D->E, E->C is a minimal cover for
the set of functional dependencies
AB->C, D->E, AB->E, E->C.
Which one of the following is CORRECT?
Question 8
The maximum number of superkeys for the relation schema R(E,F,G,H) with E as the key is
Question 9
Given the STUDENTS relation as shown below.
[caption width="800"]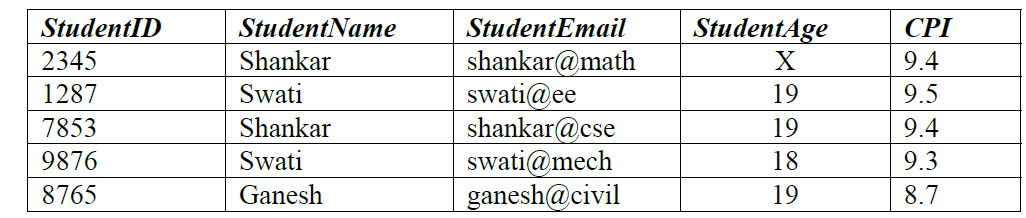 [/caption]
[/caption]
For (StudentName, StudentAge) to be the key for this instance, the value X should not be equal to
There are 89 questions to complete.
Last Updated :
Take a part in the ongoing discussion