Data Structures and Algorithms | Set 32
Last Updated :
13 Dec, 2022
Following questions have been asked in GATE CS 2014 exam.
1) Let G be a graph with n vertices and m edges. What is the tightest upper bound on the running time on Depth First Search of G? Assume that the graph is represented using adjacency matrix.
(A) O(n)
(B) O(m+n)
(C) O(n2)
(D) O(mn)
Answer: (C)
Explanation: Depth First Search of a graph takes O(m+n) time when the graph is represented using adjacency list.
In adjacency matrix representation, graph is represented as an “n x n” matrix. To do DFS, for every vertex, we traverse the row corresponding to that vertex to find all adjacent vertices (In adjacency list representation we traverse only the adjacent vertices of the vertex). Therefore time complexity becomes O(n2)
2) Consider a rooted Binary tree represented using pointers. The best upper bound on the time required to determine the number of subtrees having having exactly 4 nodes O(na Logn b). Then the value of a + 10b is ________
Answer: 1
Explanation: We can find the subtree with 4 nodes in O(n) time. Following can be a simple approach.
1) Traverse the tree in bottom up manner and find size of subtree rooted with current node
2) If size becomes 4, then print the current node.
int print4Subtree(struct Node *root)
{
if (root == NULL)
return 0;
int l = print4Subtree(root->left);
int r = print4Subtree(root->right);
if ((l + r + 1) == 4)
printf("%d ", root->data);
return (l + r + 1);
}
|
3) Consider the directed graph given below. Which one of the following is TRUE?
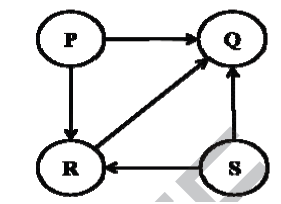
(A) The graph doesn’t have any topological ordering
(B) Both PQRS and SRPQ are topological ordering
(C) Both PSRQ and SPRQ are topological ordering
(D) PSRQ is the only topological ordering
Answer: (C)
Explanation: The graph doesn’t contain any cycle, so there exist topological ordering.
P and S must appear before R and Q because there are edges from P to R and Q, and from S to R and Q.
See Topological Ordering for more details.
4) Let P be a QuickSort Program to sort numbers in ascending order using the first element as pivot. Let t1 and t2 be the number of comparisons made by P for the inputs {1, 2, 3, 4, 5} and {4, 1, 5, 3, 2} respectively. Which one of the following holds?
(A) t1 = 5
(B) t1 < t2
(C) t1 > t2
(D) t1 = t2
Answer: (C)
Explanation: When first element or last element is chosen as pivot, Quick Sort‘s worst case occurs for the sorted arrays.
In every step of quick sort, numbers are divided as per the following recurrence.
T(n) = T(n-1) + O(n)
5) Consider the following C function in which size is the number of elements in the array E:
The value returned by the function MyX is the
int MyX(int *E, unsigned int size)
{
int Y = 0;
int Z;
int i, j, k;
for (i = 0; i < size; i++)
Y = Y + E[i];
for (i = 0; i < size; i++)
for (j = i; j < size; j++)
{
Z = 0;
for (k = i; k <= j; k++)
Z = Z + E[k];
if (Z > Y)
Y = Z;
}
return Y;
}
|
(A) maximum possible sum of elements in any sub-array of array E.
(B) maximum element in any sub-array of array E.
(C) sum of the maximum elements in all possible sub-arrays of array E
(D) the sum of all the elements in the array E.
Answer: (A)
Explanation: The function does following
Y is used to store maximum sum seen so far and Z is used to store current sum
1) Initialize Y as sum of all elements
2) For every element, calculate sum of all subarrays starting with arr[i]. Store the current sum in Z. If Z is greater than Y, then update Y.
See following for complete solutions of all GATE CS 2014 papers
GATE-CS-2014-(Set-1)
GATE-CS-2014-(Set-2)
GATE-CS-2014-(Set-3)
Please write comments if you find any of the answers/explanations incorrect, or you want to share more information about the topics discussed above.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...