In this article, we will discuss how to do data analysis with Python. We will discuss all sorts of data analysis i.e. analyzing numerical data with NumPy, Tabular data with Pandas, data visualization Matplotlib, and Exploratory data analysis.
Data Analysis With Python
Data Analysis is the technique of collecting, transforming, and organizing data to make future predictions and informed data-driven decisions. It also helps to find possible solutions for a business problem. There are six steps for Data Analysis. They are:
- Ask or Specify Data Requirements
- Prepare or Collect Data
- Clean and Process
- Analyze
- Share
- Act or Report

Data Analysis with Python
Note: To know more about these steps refer to our Six Steps of Data Analysis Process tutorial.
Analyzing Numerical Data with NumPy
NumPy is an array processing package in Python and provides a high-performance multidimensional array object and tools for working with these arrays. It is the fundamental package for scientific computing with Python.
Arrays in NumPy
NumPy Array is a table of elements (usually numbers), all of the same types, indexed by a tuple of positive integers. In Numpy, the number of dimensions of the array is called the rank of the array. A tuple of integers giving the size of the array along each dimension is known as the shape of the array.
Creating NumPy Array
NumPy arrays can be created in multiple ways, with various ranks. It can also be created with the use of different data types like lists, tuples, etc. The type of the resultant array is deduced from the type of elements in the sequences. NumPy offers several functions to create arrays with initial placeholder content. These minimize the necessity of growing arrays, an expensive operation.
Create Array using numpy.empty(shape, dtype=float, order=’C’)
Python3
import numpy as np
b = np.empty(2, dtype = int)
print("Matrix b : \n", b)
a = np.empty([2, 2], dtype = int)
print("\nMatrix a : \n", a)
c = np.empty([3, 3])
print("\nMatrix c : \n", c)
Output:

Empty Matrix using pandas
Create Array using numpy.zeros(shape, dtype = None, order = ‘C’)
Python3
import numpy as np
b = np.zeros(2, dtype = int)
print("Matrix b : \n", b)
a = np.zeros([2, 2], dtype = int)
print("\nMatrix a : \n", a)
c = np.zeros([3, 3])
print("\nMatrix c : \n", c)
Output:
Matrix b :
[0 0]
Matrix a :
[[0 0]
[0 0]]
Matrix c :
[[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]]
Operations on Numpy Arrays
Arithmetic Operations
Python3
import numpy as np
# Defining both the matrices
a = np.array([5, 72, 13, 100])
b = np.array([2, 5, 10, 30])
# Performing addition using arithmetic operator
add_ans = a+b
print(add_ans)
# Performing addition using numpy function
add_ans = np.add(a, b)
print(add_ans)
# The same functions and operations can be used for
# multiple matrices
c = np.array([1, 2, 3, 4])
add_ans = a+b+c
print(add_ans)
add_ans = np.add(a, b, c)
print(add_ans)
Output:
[ 7 77 23 130]
[ 7 77 23 130]
[ 8 79 26 134]
[ 7 77 23 130]
Python3
import numpy as np
# Defining both the matrices
a = np.array([5, 72, 13, 100])
b = np.array([2, 5, 10, 30])
# Performing subtraction using arithmetic operator
sub_ans = a-b
print(sub_ans)
# Performing subtraction using numpy function
sub_ans = np.subtract(a, b)
print(sub_ans)
Output:
[ 3 67 3 70]
[ 3 67 3 70]
Python3
import numpy as np
# Defining both the matrices
a = np.array([5, 72, 13, 100])
b = np.array([2, 5, 10, 30])
# Performing multiplication using arithmetic
# operator
mul_ans = a*b
print(mul_ans)
# Performing multiplication using numpy function
mul_ans = np.multiply(a, b)
print(mul_ans)
Output:
[ 10 360 130 3000]
[ 10 360 130 3000]
Python3
import numpy as np
# Defining both the matrices
a = np.array([5, 72, 13, 100])
b = np.array([2, 5, 10, 30])
# Performing division using arithmetic operators
div_ans = a/b
print(div_ans)
# Performing division using numpy functions
div_ans = np.divide(a, b)
print(div_ans)
Output:
[ 2.5 14.4 1.3 3.33333333]
[ 2.5 14.4 1.3 3.33333333]
For more information, refer to our NumPy – Arithmetic Operations Tutorial
NumPy Array Indexing
Indexing can be done in NumPy by using an array as an index. In the case of the slice, a view or shallow copy of the array is returned but in the index array, a copy of the original array is returned. Numpy arrays can be indexed with other arrays or any other sequence with the exception of tuples. The last element is indexed by -1 second last by -2 and so on.
Python NumPy Array Indexing
Python3
# Python program to demonstrate
# the use of index arrays.
import numpy as np
# Create a sequence of integers from
# 10 to 1 with a step of -2
a = np.arange(10, 1, -2)
print("\n A sequential array with a negative step: \n",a)
# Indexes are specified inside the np.array method.
newarr = a[np.array([3, 1, 2 ])]
print("\n Elements at these indices are:\n",newarr)
Output:
A sequential array with a negative step:
[10 8 6 4 2]
Elements at these indices are:
[4 8 6]
NumPy Array Slicing
Consider the syntax x[obj] where x is the array and obj is the index. The slice object is the index in the case of basic slicing. Basic slicing occurs when obj is :
- a slice object that is of the form start: stop: step
- an integer
- or a tuple of slice objects and integers
All arrays generated by basic slicing are always the view in the original array.
Python3
# Python program for basic slicing.
import numpy as np
# Arrange elements from 0 to 19
a = np.arange(20)
print("\n Array is:\n ",a)
# a[start:stop:step]
print("\n a[-8:17:1] = ",a[-8:17:1])
# The : operator means all elements till the end.
print("\n a[10:] = ",a[10:])
Output:
Array is:
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19]
a[-8:17:1] = [12 13 14 15 16]
a[10:] = [10 11 12 13 14 15 16 17 18 19]
Ellipsis can also be used along with basic slicing. Ellipsis (…) is the number of : objects needed to make a selection tuple of the same length as the dimensions of the array.
Python3
# Python program for indexing using basic slicing with ellipsis
import numpy as np
# A 3 dimensional array.
b = np.array([[[1, 2, 3],[4, 5, 6]],
[[7, 8, 9],[10, 11, 12]]])
print(b[...,1]) #Equivalent to b[: ,: ,1 ]
Output:
[[ 2 5]
[ 8 11]]
NumPy Array Broadcasting
The term broadcasting refers to how numpy treats arrays with different Dimensions during arithmetic operations which lead to certain constraints, the smaller array is broadcast across the larger array so that they have compatible shapes.
Let’s assume that we have a large data set, each datum is a list of parameters. In Numpy we have a 2-D array, where each row is a datum and the number of rows is the size of the data set. Suppose we want to apply some sort of scaling to all these data every parameter gets its own scaling factor or say Every parameter is multiplied by some factor.
Just to have a clear understanding, let’s count calories in foods using a macro-nutrient breakdown. Roughly put, the caloric parts of food are made of fats (9 calories per gram), protein (4 CPG), and carbs (4 CPG). So if we list some foods (our data), and for each food list its macro-nutrient breakdown (parameters), we can then multiply each nutrient by its caloric value (apply scaling) to compute the caloric breakdown of every food item.
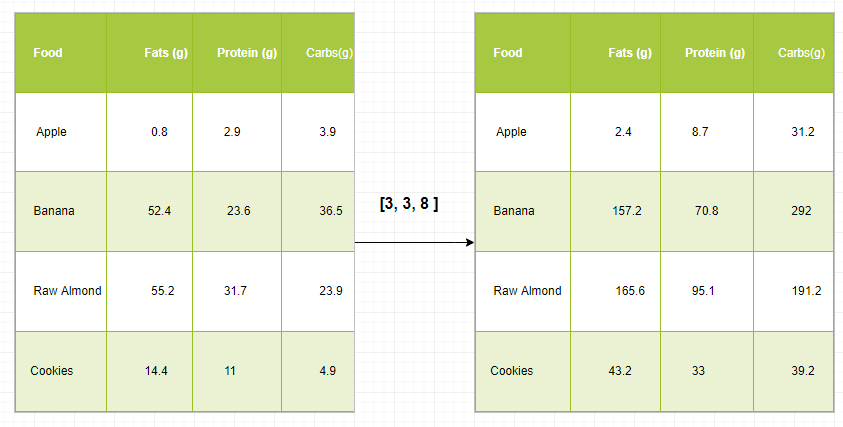
With this transformation, we can now compute all kinds of useful information. For example, what is the total number of calories present in some food or, given a breakdown of my dinner know how many calories did I get from protein and so on.
Let’s see a naive way of producing this computation with Numpy:
Python3
import numpy as np
macros = np.array([
[0.8, 2.9, 3.9],
[52.4, 23.6, 36.5],
[55.2, 31.7, 23.9],
[14.4, 11, 4.9]
])
# Create a new array filled with zeros,
# of the same shape as macros.
result = np.zeros_like(macros)
cal_per_macro = np.array([3, 3, 8])
# Now multiply each row of macros by
# cal_per_macro. In Numpy, `*` is
# element-wise multiplication between two arrays.
for i in range(macros.shape[0]):
result[i, :] = macros[i, :] * cal_per_macro
result
Output:
array([[ 2.4, 8.7, 31.2],
[157.2, 70.8, 292. ],
[165.6, 95.1, 191.2],
[ 43.2, 33. , 39.2]])
Broadcasting Rules: Broadcasting two arrays together follow these rules:
- If the arrays don’t have the same rank then prepend the shape of the lower rank array with 1s until both shapes have the same length.
- The two arrays are compatible in a dimension if they have the same size in the dimension or if one of the arrays has size 1 in that dimension.
- The arrays can be broadcast together if they are compatible with all dimensions.
- After broadcasting, each array behaves as if it had a shape equal to the element-wise maximum of shapes of the two input arrays.
- In any dimension where one array had a size of 1 and the other array had a size greater than 1, the first array behaves as if it were copied along that dimension.
Python3
import numpy as np
v = np.array([12, 24, 36])
w = np.array([45, 55])
# To compute an outer product we first
# reshape v to a column vector of shape 3x1
# then broadcast it against w to yield an output
# of shape 3x2 which is the outer product of v and w
print(np.reshape(v, (3, 1)) * w)
X = np.array([[12, 22, 33], [45, 55, 66]])
# x has shape 2x3 and v has shape (3, )
# so they broadcast to 2x3,
print(X + v)
# Add a vector to each column of a matrix X has
# shape 2x3 and w has shape (2, ) If we transpose X
# then it has shape 3x2 and can be broadcast against w
# to yield a result of shape 3x2.
# Transposing this yields the final result
# of shape 2x3 which is the matrix.
print((X.T + w).T)
# Another solution is to reshape w to be a column
# vector of shape 2X1 we can then broadcast it
# directly against X to produce the same output.
print(X + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant, X has shape 2x3.
# Numpy treats scalars as arrays of shape();
# these can be broadcast together to shape 2x3.
print(X * 2)
Output:
[[ 540 660]
[1080 1320]
[1620 1980]]
[[ 24 46 69]
[ 57 79 102]]
[[ 57 67 78]
[100 110 121]]
[[ 57 67 78]
[100 110 121]]
[[ 24 44 66]
[ 90 110 132]]
Note: For more information, refer to our Python NumPy Tutorial.
Analyzing Data Using Pandas
Python Pandas Is used for relational or labeled data and provides various data structures for manipulating such data and time series. This library is built on top of the NumPy library. This module is generally imported as:
import pandas as pd
Here, pd is referred to as an alias to the Pandas. However, it is not necessary to import the library using the alias, it just helps in writing less amount code every time a method or property is called. Pandas generally provide two data structures for manipulating data, They are:
Series:
Pandas Series is a one-dimensional labeled array capable of holding data of any type (integer, string, float, python objects, etc.). The axis labels are collectively called indexes. Pandas Series is nothing but a column in an excel sheet. Labels need not be unique but must be a hashable type. The object supports both integer and label-based indexing and provides a host of methods for performing operations involving the index.
.webp)
Pandas Series
It can be created using the Series() function by loading the dataset from the existing storage like SQL, Database, CSV Files, Excel Files, etc., or from data structures like lists, dictionaries, etc.
Python Pandas Creating Series
Python3
import pandas as pd
import numpy as np
# Creating empty series
ser = pd.Series()
print(ser)
# simple array
data = np.array(['g', 'e', 'e', 'k', 's'])
ser = pd.Series(data)
print(ser)
Output:

pnadas series
Dataframe:
Pandas DataFrame is a two-dimensional size-mutable, potentially heterogeneous tabular data structure with labeled axes (rows and columns). A Data frame is a two-dimensional data structure, i.e., data is aligned in a tabular fashion in rows and columns. Pandas DataFrame consists of three principal components, the data, rows, and columns.
.webp)
Pandas Dataframe
It can be created using the Dataframe() method and just like a series, it can also be from different file types and data structures.
Python Pandas Creating Dataframe
Python3
import pandas as pd
# Calling DataFrame constructor
df = pd.DataFrame()
print(df)
# list of strings
lst = ['Geeks', 'For', 'Geeks', 'is',
'portal', 'for', 'Geeks']
# Calling DataFrame constructor on list
df = pd.DataFrame(lst)
df
Output:

Creating Dataframe from python list
Creating Dataframe from CSV
We can create a dataframe from the CSV files using the read_csv() function.
Python Pandas read CSV
Python3
import pandas as pd
# Reading the CSV file
df = pd.read_csv("Iris.csv")
# Printing top 5 rows
df.head()
Output:

head of a dataframe
Filtering DataFrame
Pandas dataframe.filter() function is used to Subset rows or columns of dataframe according to labels in the specified index. Note that this routine does not filter a dataframe on its contents. The filter is applied to the labels of the index.
Python Pandas Filter Dataframe
Python3
import pandas as pd
# Reading the CSV file
df = pd.read_csv("Iris.csv")
# applying filter function
df.filter(["Species", "SepalLengthCm", "SepalLengthCm"]).head()
Output:

Applying filter on dataset
Sorting DataFrame
In order to sort the data frame in pandas, the function sort_values() is used. Pandas sort_values() can sort the data frame in Ascending or Descending order.
Python Pandas Sorting Dataframe in Ascending Order
Output:

Sorted dataset based on a column value
Pandas GroupBy
Groupby is a pretty simple concept. We can create a grouping of categories and apply a function to the categories. In real data science projects, you’ll be dealing with large amounts of data and trying things over and over, so for efficiency, we use the Groupby concept. Groupby mainly refers to a process involving one or more of the following steps they are:
- Splitting: It is a process in which we split data into group by applying some conditions on datasets.
- Applying: It is a process in which we apply a function to each group independently.
- Combining: It is a process in which we combine different datasets after applying groupby and results into a data structure.
The following image will help in understanding the process involve in the Groupby concept.
1. Group the unique values from the Team column

Pandas Groupby Method
2. Now there’s a bucket for each group

3. Toss the other data into the buckets

4. Apply a function on the weight column of each bucket.

Applying Function on the weight column of each column
Python Pandas GroupBy
Python3
# importing pandas module
import pandas as pd
# Define a dictionary containing employee data
data1 = {'Name': ['Jai', 'Anuj', 'Jai', 'Princi',
'Gaurav', 'Anuj', 'Princi', 'Abhi'],
'Age': [27, 24, 22, 32,
33, 36, 27, 32],
'Address': ['Nagpur', 'Kanpur', 'Allahabad', 'Kannuaj',
'Jaunpur', 'Kanpur', 'Allahabad', 'Aligarh'],
'Qualification': ['Msc', 'MA', 'MCA', 'Phd',
'B.Tech', 'B.com', 'Msc', 'MA']}
# Convert the dictionary into DataFrame
df = pd.DataFrame(data1)
print("Original Dataframe")
display(df)
# applying groupby() function to
# group the data on Name value.
gk = df.groupby('Name')
# Let's print the first entries
# in all the groups formed.
print("After Creating Groups")
gk.first()
Output:

pandas groupby
Applying function to group:
After splitting a data into a group, we apply a function to each group in order to do that we perform some operations they are:
- Aggregation: It is a process in which we compute a summary statistic (or statistics) about each group. For Example, Compute group sums or means
- Transformation: It is a process in which we perform some group-specific computations and return a like-indexed. For Example, Filling NAs within groups with a value derived from each group
- Filtration: It is a process in which we discard some groups, according to a group-wise computation that evaluates True or False. For Example, Filtering out data based on the group sum or mean
Pandas Aggregation
Aggregation is a process in which we compute a summary statistic about each group. The aggregated function returns a single aggregated value for each group. After splitting data into groups using groupby function, several aggregation operations can be performed on the grouped data.
Python Pandas Aggregation
Python3
# importing pandas module
import pandas as pd
# importing numpy as np
import numpy as np
# Define a dictionary containing employee data
data1 = {'Name': ['Jai', 'Anuj', 'Jai', 'Princi',
'Gaurav', 'Anuj', 'Princi', 'Abhi'],
'Age': [27, 24, 22, 32,
33, 36, 27, 32],
'Address': ['Nagpur', 'Kanpur', 'Allahabad', 'Kannuaj',
'Jaunpur', 'Kanpur', 'Allahabad', 'Aligarh'],
'Qualification': ['Msc', 'MA', 'MCA', 'Phd',
'B.Tech', 'B.com', 'Msc', 'MA']}
# Convert the dictionary into DataFrame
df = pd.DataFrame(data1)
# performing aggregation using
# aggregate method
grp1 = df.groupby('Name')
grp1.aggregate(np.sum)
Output:

Use of sum aggregate function on dataset
Concatenating DataFrame
In order to concat the dataframe, we use concat() function which helps in concatenating the dataframe. This function does all the heavy lifting of performing concatenation operations along with an axis of Pandas objects while performing optional set logic (union or intersection) of the indexes (if any) on the other axes.
Python Pandas Concatenate Dataframe
Python3
# importing pandas module
import pandas as pd
# Define a dictionary containing employee data
data1 = {'key': ['K0', 'K1', 'K2', 'K3'],
'Name':['Jai', 'Princi', 'Gaurav', 'Anuj'],
'Age':[27, 24, 22, 32],}
# Define a dictionary containing employee data
data2 = {'key': ['K0', 'K1', 'K2', 'K3'],
'Address':['Nagpur', 'Kanpur', 'Allahabad', 'Kannuaj'],
'Qualification':['Btech', 'B.A', 'Bcom', 'B.hons']}
# Convert the dictionary into DataFrame
df = pd.DataFrame(data1)
# Convert the dictionary into DataFrame
df1 = pd.DataFrame(data2)
display(df, df1)
# combining series and dataframe
res = pd.concat([df, df1], axis=1)
res
Output:

Merging DataFrame
When we need to combine very large DataFrames, joins serve as a powerful way to perform these operations swiftly. Joins can only be done on two DataFrames at a time, denoted as left and right tables. The key is the common column that the two DataFrames will be joined on. It’s a good practice to use keys that have unique values throughout the column to avoid unintended duplication of row values. Pandas provide a single function, merge(), as the entry point for all standard database join operations between DataFrame objects.
There are four basic ways to handle the join (inner, left, right, and outer), depending on which rows must retain their data.
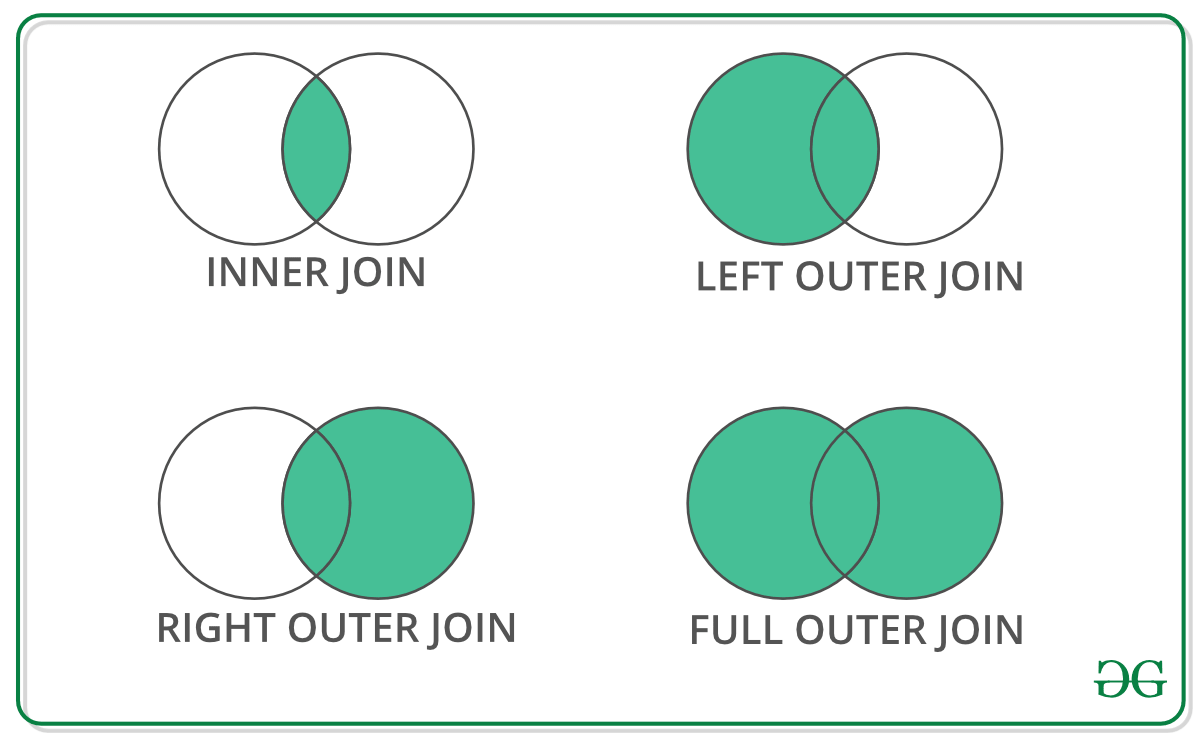
Python Pandas Merge Dataframe
Python3
# importing pandas module
import pandas as pd
# Define a dictionary containing employee data
data1 = {'key': ['K0', 'K1', 'K2', 'K3'],
'Name':['Jai', 'Princi', 'Gaurav', 'Anuj'],
'Age':[27, 24, 22, 32],}
# Define a dictionary containing employee data
data2 = {'key': ['K0', 'K1', 'K2', 'K3'],
'Address':['Nagpur', 'Kanpur', 'Allahabad', 'Kannuaj'],
'Qualification':['Btech', 'B.A', 'Bcom', 'B.hons']}
# Convert the dictionary into DataFrame
df = pd.DataFrame(data1)
# Convert the dictionary into DataFrame
df1 = pd.DataFrame(data2)
display(df, df1)
# using .merge() function
res = pd.merge(df, df1, on='key')
res
Output:

Concatinating Two datasets
Joining DataFrame
In order to join the dataframe, we use .join() function this function is used for combining the columns of two potentially differently indexed DataFrames into a single result DataFrame.
Python Pandas Join Dataframe
Python3
# importing pandas module
import pandas as pd
# Define a dictionary containing employee data
data1 = {'Name':['Jai', 'Princi', 'Gaurav', 'Anuj'],
'Age':[27, 24, 22, 32]}
# Define a dictionary containing employee data
data2 = {'Address':['Allahabad', 'Kannuaj', 'Allahabad', 'Kannuaj'],
'Qualification':['MCA', 'Phd', 'Bcom', 'B.hons']}
# Convert the dictionary into DataFrame
df = pd.DataFrame(data1,index=['K0', 'K1', 'K2', 'K3'])
# Convert the dictionary into DataFrame
df1 = pd.DataFrame(data2, index=['K0', 'K2', 'K3', 'K4'])
display(df, df1)
# joining dataframe
res = df.join(df1)
res
Output:

Joining two datasets
For more information, refer to our Pandas Merging, Joining, and Concatenating tutorial
For a complete guide on Pandas refer to our Pandas Tutorial.
Visualization with Matplotlib
Matplotlib is easy to use and an amazing visualizing library in Python. It is built on NumPy arrays and designed to work with the broader SciPy stack and consists of several plots like line, bar, scatter, histogram, etc.
Pyplot
Pyplot is a Matplotlib module that provides a MATLAB-like interface. Pyplot provides functions that interact with the figure i.e. creates a figure, decorates the plot with labels, and creates a plotting area in a figure.
Python3
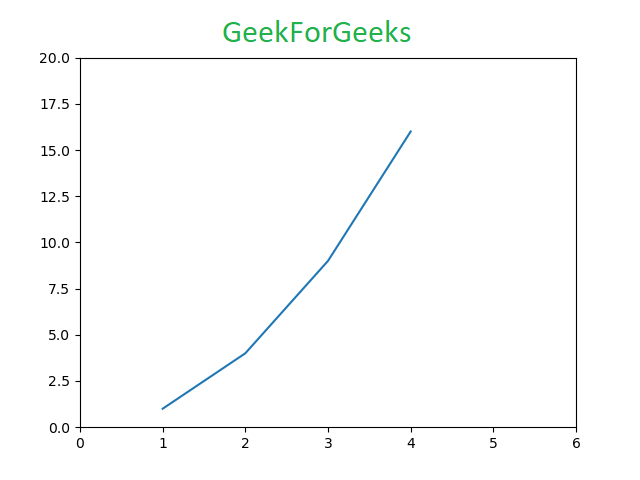
# Python program to show pyplot module
import matplotlib.pyplot as plt
plt.plot([1, 2, 3, 4], [1, 4, 9, 16])
plt.axis([0, 6, 0, 20])
plt.show()
Output:
Bar chart
A bar plot or bar chart is a graph that represents the category of data with rectangular bars with lengths and heights that is proportional to the values which they represent. The bar plots can be plotted horizontally or vertically. A bar chart describes the comparisons between the discrete categories. It can be created using the bar() method.
Python Matplotlib Bar Chart
Here we will use the iris dataset only
Python3
import matplotlib.pyplot as plt
import pandas as pd
df = pd.read_csv("Iris.csv")
# This will plot a simple bar chart
plt.bar(df['Species'], df['SepalLengthCm'])
# Title to the plot
plt.title("Iris Dataset")
# Adding the legends
plt.legend(["bar"])
plt.show()
Output:

Bar chart using matplotlib library
Histograms
A histogram is basically used to represent data in the form of some groups. It is a type of bar plot where the X-axis represents the bin ranges while the Y-axis gives information about frequency. To create a histogram the first step is to create a bin of the ranges, then distribute the whole range of the values into a series of intervals, and count the values which fall into each of the intervals. Bins are clearly identified as consecutive, non-overlapping intervals of variables. The hist() function is used to compute and create a histogram of x.
Python Matplotlib Histogram
Python3
import matplotlib.pyplot as plt
import pandas as pd
df = pd.read_csv("Iris.csv")
plt.hist(df["SepalLengthCm"])
# Title to the plot
plt.title("Histogram")
# Adding the legends
plt.legend(["SepalLengthCm"])
plt.show()
Output:

Histplot using matplotlib library
Scatter Plot
Scatter plots are used to observe relationship between variables and uses dots to represent the relationship between them. The scatter() method in the matplotlib library is used to draw a scatter plot.
Python Matplotlib Scatter Plot
Python3
import matplotlib.pyplot as plt
import pandas as pd
df = pd.read_csv("Iris.csv")
plt.scatter(df["Species"], df["SepalLengthCm"])
# Title to the plot
plt.title("Scatter Plot")
# Adding the legends
plt.legend(["SepalLengthCm"])
plt.show()
Output:

Scatter plot using matplotlib library
Box Plot
A boxplot,Correlation also known as a box and whisker plot. It is a very good visual representation when it comes to measuring the data distribution. Clearly plots the median values, outliers and the quartiles. Understanding data distribution is another important factor which leads to better model building. If data has outliers, box plot is a recommended way to identify them and take necessary actions. The box and whiskers chart shows how data is spread out. Five pieces of information are generally included in the chart
- The minimum is shown at the far left of the chart, at the end of the left ‘whisker’
- First quartile, Q1, is the far left of the box (left whisker)
- The median is shown as a line in the center of the box
- Third quartile, Q3, shown at the far right of the box (right whisker)
- The maximum is at the far right of the box
Representation of box plot

Inter quartile range

Illustrating box plot
Python Matplotlib Box Plot
Python3
import matplotlib.pyplot as plt
import pandas as pd
df = pd.read_csv("Iris.csv")
plt.boxplot(df["SepalWidthCm"])
# Title to the plot
plt.title("Box Plot")
# Adding the legends
plt.legend(["SepalWidthCm"])
plt.show()
Output:

Boxplot using matplotlib library
Correlation Heatmaps
A 2-D Heatmap is a data visualization tool that helps to represent the magnitude of the phenomenon in form of colors. A correlation heatmap is a heatmap that shows a 2D correlation matrix between two discrete dimensions, using colored cells to represent data from usually a monochromatic scale. The values of the first dimension appear as the rows of the table while the second dimension is a column. The color of the cell is proportional to the number of measurements that match the dimensional value. This makes correlation heatmaps ideal for data analysis since it makes patterns easily readable and highlights the differences and variation in the same data. A correlation heatmap, like a regular heatmap, is assisted by a colorbar making data easily readable and comprehensible.
Note: The data here has to be passed with corr() method to generate a correlation heatmap. Also, corr() itself eliminates columns that will be of no use while generating a correlation heatmap and selects those which can be used.
Python Matplotlib Correlation Heatmap
Python3
import matplotlib.pyplot as plt
import pandas as pd
df = pd.read_csv("Iris.csv")
plt.imshow(df.corr() , cmap = 'autumn' , interpolation = 'nearest' )
plt.title("Heat Map")
plt.show()
Output:

Heatmap using matplotlib library
For more information on data visualization refer to our below tutorials –
Exploratory Data Analysis
Exploratory Data Analysis (EDA) is a technique to analyze data using some visual Techniques. With this technique, we can get detailed information about the statistical summary of the data. We will also be able to deal with the duplicates values, outliers, and also see some trends or patterns present in the dataset.
Note: We will be using Iris Dataset.
Getting Information about the Dataset
We will use the shape parameter to get the shape of the dataset.
Shape of Dataframe
Python3
df.shape
Output:
(150, 6)
We can see that the dataframe contains 6 columns and 150 rows.
Now, let’s also the columns and their data types. For this, we will use the info() method.
Information about Dataset
Python3
df.info()
Output:

information about the dataset
We can see that only one column has categorical data and all the other columns are of the numeric type with non-Null entries.
Let’s get a quick statistical summary of the dataset using the describe() method. The describe() function applies basic statistical computations on the dataset like extreme values, count of data points standard deviation, etc. Any missing value or NaN value is automatically skipped. describe() function gives a good picture of the distribution of data.
Description of dataset
Python3
df.describe()
Output:

Description about the dataset
We can see the count of each column along with their mean value, standard deviation, minimum and maximum values.
Checking Missing Values
We will check if our data contains any missing values or not. Missing values can occur when no information is provided for one or more items or for a whole unit. We will use the isnull() method.
python code for missing value
Python3
df.isnull().sum()
Output:

Missing values in the dataset
We can see that no column has any missing value.
Checking Duplicates
Let’s see if our dataset contains any duplicates or not. Pandas drop_duplicates() method helps in removing duplicates from the data frame.
Pandas function for missing values
Python3
data = df.drop_duplicates(subset ="Species",)
data
Output:

Dropping duplicate value in the dataset
We can see that there are only three unique species. Let’s see if the dataset is balanced or not i.e. all the species contain equal amounts of rows or not. We will use the Series.value_counts() function. This function returns a Series containing counts of unique values.
Python code for value counts in the column
Python3
df.value_counts("Species")
Output:

value count in the dataset
We can see that all the species contain an equal amount of rows, so we should not delete any entries.
Relation between variables
We will see the relationship between the sepal length and sepal width and also between petal length and petal width.
Comparing Sepal Length and Sepal Width
Python3
# importing packages
import seaborn as sns
import matplotlib.pyplot as plt
sns.scatterplot(x='SepalLengthCm', y='SepalWidthCm',
hue='Species', data=df, )
# Placing Legend outside the Figure
plt.legend(bbox_to_anchor=(1, 1), loc=2)
plt.show()
Output:

Scatter plot using matplotlib library
From the above plot, we can infer that –
- Species Setosa has smaller sepal lengths but larger sepal widths.
- Versicolor Species lies in the middle of the other two species in terms of sepal length and width
- Species Virginica has larger sepal lengths but smaller sepal widths.
Comparing Petal Length and Petal Width
Python3
# importing packages
import seaborn as sns
import matplotlib.pyplot as plt
sns.scatterplot(x='PetalLengthCm', y='PetalWidthCm',
hue='Species', data=df, )
# Placing Legend outside the Figure
plt.legend(bbox_to_anchor=(1, 1), loc=2)
plt.show()
Output:

sactter plot petal length
From the above plot, we can infer that –
- The species Setosa has smaller petal lengths and widths.
- Versicolor Species lies in the middle of the other two species in terms of petal length and width
- Species Virginica has the largest petal lengths and widths.
Let’s plot all the column’s relationships using a pairplot. It can be used for multivariate analysis.
Python code for pairplot
Python3
# importing packages
import seaborn as sns
import matplotlib.pyplot as plt
sns.pairplot(df.drop(['Id'], axis = 1),
hue='Species', height=2)
Output:
.webp)
Pairplot for the dataset
We can see many types of relationships from this plot such as the species Seotsa has the smallest of petals widths and lengths. It also has the smallest sepal length but larger sepal widths. Such information can be gathered about any other species.
Handling Correlation
Pandas dataframe.corr() is used to find the pairwise correlation of all columns in the dataframe. Any NA values are automatically excluded. Any non-numeric data type columns in the dataframe are ignored.
Example:
Python3
data.corr(method='pearson')
Output:

correlation between columns in the dataset
Heatmaps
The heatmap is a data visualization technique that is used to analyze the dataset as colors in two dimensions. Basically, it shows a correlation between all numerical variables in the dataset. In simpler terms, we can plot the above-found correlation using the heatmaps.
python code for heatmap
Python3
# importing packages
import seaborn as sns
import matplotlib.pyplot as plt
sns.heatmap(df.corr(method='pearson').drop(
['Id'], axis=1).drop(['Id'], axis=0),
annot = True);
plt.show()
Output:

Heatmap for correlation in the dataset
From the above graph, we can see that –
- Petal width and petal length have high correlations.
- Petal length and sepal width have good correlations.
- Petal Width and Sepal length have good correlations.
Handling Outliers
An Outlier is a data item/object that deviates significantly from the rest of the (so-called normal)objects. They can be caused by measurement or execution errors. The analysis for outlier detection is referred to as outlier mining. There are many ways to detect outliers, and the removal process is the data frame same as removing a data item from the panda’s dataframe.
Let’s consider the iris dataset and let’s plot the boxplot for the SepalWidthCm column.
python code for Boxplot
Python3
# importing packages
import seaborn as sns
import matplotlib.pyplot as plt
# Load the dataset
df = pd.read_csv('Iris.csv')
sns.boxplot(x='SepalWidthCm', data=df)
Output:

Boxplot for sepalwidth column
In the above graph, the values above 4 and below 2 are acting as outliers.
Removing Outliers
For removing the outlier, one must follow the same process of removing an entry from the dataset using its exact position in the dataset because in all the above methods of detecting the outliers end result is the list of all those data items that satisfy the outlier definition according to the method used.
We will detect the outliers using IQR and then we will remove them. We will also draw the boxplot to see if the outliers are removed or not.
Python3
# Importing
import sklearn
from sklearn.datasets import load_boston
import pandas as pd
import seaborn as sns
# Load the dataset
df = pd.read_csv('Iris.csv')
# IQR
Q1 = np.percentile(df['SepalWidthCm'], 25,
interpolation = 'midpoint')
Q3 = np.percentile(df['SepalWidthCm'], 75,
interpolation = 'midpoint')
IQR = Q3 - Q1
print("Old Shape: ", df.shape)
# Upper bound
upper = np.where(df['SepalWidthCm'] >= (Q3+1.5*IQR))
# Lower bound
lower = np.where(df['SepalWidthCm'] <= (Q1-1.5*IQR))
# Removing the Outliers
df.drop(upper[0], inplace = True)
df.drop(lower[0], inplace = True)
print("New Shape: ", df.shape)
sns.boxplot(x='SepalWidthCm', data=df)
Output:

boxplot using seaborn library
For more information about EDA, refer to our below tutorials –
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...