C# Program for Program for array rotation
Last Updated :
17 Aug, 2023
Write a function rotate(ar[], d, n) that rotates arr[] of size n by d elements.
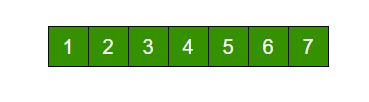
Rotation of the above array by 2 will make array

METHOD 1 (Using temp array)
Input arr[] = [1, 2, 3, 4, 5, 6, 7], d = 2, n =7
1) Store the first d elements in a temp array
temp[] = [1, 2]
2) Shift rest of the arr[]
arr[] = [3, 4, 5, 6, 7, 6, 7]
3) Store back the d elements
arr[] = [3, 4, 5, 6, 7, 1, 2]
Time complexity : O(n)
Auxiliary Space : O(d)
METHOD 2 (Rotate one by one)
leftRotate(arr[], d, n)
start
For i = 0 to i < d
Left rotate all elements of arr[] by one
end
To rotate by one, store arr[0] in a temporary variable temp, move arr[1] to arr[0], arr[2] to arr[1] …and finally temp to arr[n-1]
Let us take the same example arr[] = [1, 2, 3, 4, 5, 6, 7], d = 2
Rotate arr[] by one 2 times
We get [2, 3, 4, 5, 6, 7, 1] after first rotation and [ 3, 4, 5, 6, 7, 1, 2] after second rotation.
Below is the implementation of the above approach :
C#
using System;
class GFG {
static void leftRotate(int[] arr, int d,
int n)
{
for (int i = 0; i < d; i++)
leftRotatebyOne(arr, n);
}
static void leftRotatebyOne(int[] arr, int n)
{
int i, temp = arr[0];
for (i = 0; i < n - 1; i++)
arr[i] = arr[i + 1];
arr[n-1] = temp;
}
static void printArray(int[] arr, int size)
{
for (int i = 0; i < size; i++)
Console.Write(arr[i] + " ");
}
public static void Main()
{
int[] arr = { 1, 2, 3, 4, 5, 6, 7 };
leftRotate(arr, 2, 7);
printArray(arr, 7);
}
}
|
Output :
3 4 5 6 7 1 2
Time complexity : O(n * d)
Auxiliary Space : O(1)
METHOD 3 (A Juggling Algorithm)
This is an extension of method 2. Instead of moving one by one, divide the array in different sets
where number of sets is equal to GCD of n and d and move the elements within sets.
If GCD is 1 as is for the above example array (n = 7 and d =2), then elements will be moved within one set only, we just start with temp = arr[0] and keep moving arr[I+d] to arr[I] and finally store temp at the right place.
Here is an example for n =12 and d = 3. GCD is 3 and
Let arr[] be {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
a) Elements are first moved in first set – (See below
diagram for this movement)
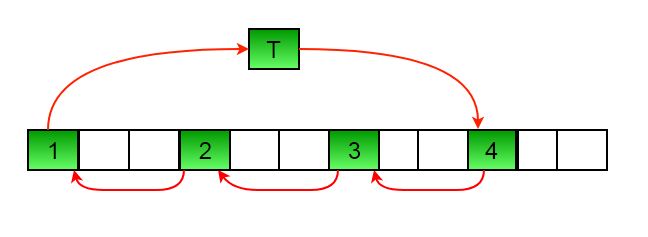
arr[] after this step --> {4 2 3 7 5 6 10 8 9 1 11 12}
b) Then in second set.
arr[] after this step --> {4 5 3 7 8 6 10 11 9 1 2 12}
c) Finally in third set.
arr[] after this step --> {4 5 6 7 8 9 10 11 12 1 2 3}
Below is the implementation of the above approach :
C#
using System;
class GFG {
static void leftRotate(int[] arr, int d,
int n)
{
int i, j, k, temp;
d = d % n;
int g_c_d = gcd(d, n);
for (i = 0; i < g_c_d; i++) {
temp = arr[i];
j = i;
while (true) {
k = j + d;
if (k >= n)
k = k - n;
if (k == i)
break;
arr[j] = arr[k];
j = k;
}
arr[j] = temp;
}
}
static void printArray(int[] arr, int size)
{
for (int i = 0; i < size; i++)
Console.Write(arr[i] + " ");
}
static int gcd(int a, int b)
{
if (b == 0)
return a;
else
return gcd(b, a % b);
}
public static void Main()
{
int[] arr = { 1, 2, 3, 4, 5, 6, 7 };
leftRotate(arr, 2, 7);
printArray(arr, 7);
}
}
|
Output :
3 4 5 6 7 1 2
Time complexity : O(n)
Auxiliary Space : O(1)
Please see following posts for other methods of array rotation:
Block swap algorithm for array rotation
Reversal algorithm for array rotation
Please write comments if you find any bug in above programs/algorithms.
Please refer complete article on Program for array rotation for more details!
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...