Cross Product of Vectors in R Programming

In mathematics, the cross product or also known as the vector product is a binary operation on two vectors in three-dimensional space and is denoted by the symbol ‘X‘. Given two linearly independent vectors a and b, the cross product, a × b is a vector that is perpendicular to both a and b and thus normal to the plane containing them.

Let we have given two vectors,

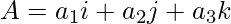
and,

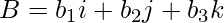
where,

i: the unit vector along the x directions

j: the unit vector along the y directions

k: the unit vector along the z directions

Then the cross product is calculated as:

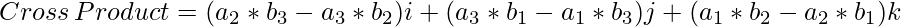
where,

are the coefficient of unit vector along i, j and k directions.

Example:

Given two vectors A and B as,

A = 3i + 5j + 4k,

and

B = 2i + 7j + 5k

Cross Product = (5 ? 5 – 4 ? 7)i + (4 ? 2 – 3 ? 5)j + (3 ? 7 – 5 ? 2)k  

                      = (?3)i + (?7)j + (11)k

Computing Cross Product in R

R language provides a very efficient method to calculate the cross product of two vectors. By using cross() method which is available in the pracma library. This function computes the cross or vector product of vectors in 3 dimensions. In the case of matrices, it takes the first dimension of length 3 and computes the cross product between corresponding columns or rows.

Syntax: cross(x, y)

Parameters:

x: numeric vector or matrix

y: numeric vector or matrix

# Taking Input as Vectors

Example 1:

R

# R Program illustrating
# cross product of two vectors

# Import the required library
library(pracma)

# Taking two vectors
a = c(3, 5, 4)
b = c(2, 7, 5)

# Calculating cross product using cross()
print(cross(a, b))

Output:

[1] -3 -7 11

Example 2:

R

# R Program illustrating
# cross product of two vectors

# Import the required library
library(pracma)

# Taking two vectors
a = c(23, 15, 49)
b = c(28, 17, 25)

# Calculating cross product using cross()
print(cross(a, b))

Output:

[1] -458  797  -29

# Taking Input as Matrix

Example 1:

R

# R Program illustrating
# cross product of two vectors

# Import the required library
library(pracma)

# Taking two matrices
a = matrix(
  c(1, 2, 3, 4, 5, 6, 7, 8, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)
b = matrix(
  c(5, 2, 1, 4, 6, 6, 3, 2, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)

# Calculating cross product using cross()
print(cross(a, b))

Output:

      [, 1] [, 2] [, 3]
[1, ]   -4   14   -8
[2, ]   -6    0    4
[3, ]   54  -36  -10

Example 2:

R

# R Program illustrating
# cross product of two vectors

# Import the required library
library(pracma)

# Taking two matrices
a = matrix(
  c(11, 2, 31, 4, 52, 64, 7, 8, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)
b = matrix(
  c(85, 21, 1, 4, 61, 6, 32, 2, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)

# Calculating cross product using cross()
print(cross(a, b))

Output:

      [, 1] [, 2] [, 3]
[1, ]  -649 2624   61
[2, ] -3592  232   36
[3, ]    54  225 -242