Cristian’s Algorithm

Cristian’s Algorithm is a clock synchronization algorithm is used to synchronize time with a time server by client processes. This algorithm works well with low-latency networks where Round Trip Time is short as compared to accuracy while redundancy-prone distributed systems/applications do not go hand in hand with this algorithm. Here Round Trip Time refers to the time duration between the start of a Request and the end of the corresponding Response.
Below is an illustration imitating the working of Cristian’s algorithm: 

Algorithm:
1) The process on the client machine sends the request for fetching clock time(time at the server) to the Clock Server at time .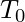
2) The Clock Server listens to the request made by the client process and returns the response in form of clock server time.
3) The client process fetches the response from the Clock Server at time 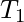and calculates the synchronized client clock time using the formula given below.

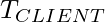
where refers to the synchronized clock time, 
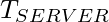
refers to the clock time returned by the server, 
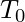
refers to the time at which request was sent by the client process, 
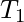
refers to the time at which response was received by the client process
Working/Reliability of the above formula: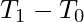
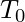
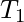
refers to the combined time taken by the network and the server to transfer the request to the server, process the request, and return the response back to the client process, assuming that the network latency and are approximately equal.
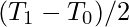
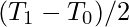
The time at the client-side differs from actual time by at most seconds. Using the above statement we can draw a conclusion that the error in synchronization can be at most seconds. 
Hence, 

Python Codes below illustrate the working of Cristian’s algorithm: 

Code below is used to initiate a prototype of a clock server on local machine: 

C++

// C++ equivalent
#include <iostream>
#include <string>
#include <chrono>
#include <ctime>
#include <sys/socket.h>

// Function used to initiate the Clock Server
void initiateClockServer() {
    // Create socket
    int socketfd = socket(AF_INET, SOCK_STREAM, 0);
    std::cout << "Socket successfully created" << std::endl;

    // Set port
    int port = 8000;

    // Bind socket to port
    struct sockaddr_in server_addr;
    server_addr.sin_family = AF_INET;
    server_addr.sin_addr.s_addr = INADDR_ANY;
    server_addr.sin_port = htons(port);
    bind(socketfd, (struct sockaddr*)&server_addr, sizeof(server_addr));
    std::cout << "Socket is listening..." << std::endl;

    // Start listening to requests
    listen(socketfd, 5);

    // Clock Server Running forever
    while (true) {
        // Establish connection with client
        struct sockaddr_in client_addr;
        int client_len = sizeof(client_addr);
        int connfd = accept(socketfd, (struct sockaddr*) &client_addr, (socklen_t*)&client_len);
        std::cout << "Server connected to " << client_addr.sin_addr.s_addr << std::endl;

        // Respond the client with server clock time
        std::chrono::time_point<std::chrono::system_clock> now = std::chrono::system_clock::now();
        std::time_t time = std::chrono::system_clock::to_time_t(now);
        std::string time_str = std::ctime(&time);
        send(connfd, time_str.c_str(), time_str.size(), 0);

        // Close the connection with the client process
        close(connfd);
    }
}

// Driver function
int main() {
    // Trigger the Clock Server
    initiateClockServer();
    return 0;
}

Java

import java.net.*;
import java.io.*;
import java.util.Date;

public class ClockServer {
    // Function used to initiate the Clock Server
    public static void initiateClockServer() throws IOException
    {

        // Create socket
        ServerSocket serverSocket = new ServerSocket(8000);
        System.out.println("Socket successfully created");

        // Clock Server Running forever
        while (true)
        {

            // Start listening to requests
            System.out.println("Socket is listening...");
            Socket clientSocket = serverSocket.accept();
            System.out.println("Server connected to " + clientSocket.getInetAddress());

            // Respond the client with server clock time
            Date now = new Date();
            String timeStr = now.toString();
            OutputStream os = clientSocket.getOutputStream();
            OutputStreamWriter osw = new OutputStreamWriter(os);
            BufferedWriter bw = new BufferedWriter(osw);
            bw.write(timeStr + "\n");
            bw.flush();

            // Close the connection with the client process
            clientSocket.close();
        }
    }

    // Driver function
    public static void main(String[] args) throws IOException
    {

        // Trigger the Clock Server
        initiateClockServer();
    }
}

Python3

# Python3 program imitating a clock server

import socket
import datetime

# function used to initiate the Clock Server
def initiateClockServer():

    s = socket.socket()
    print("Socket successfully created")

    # Server port
    port = 8000

    s.bind(('', port))

    # Start listening to requests
    s.listen(5)
    print("Socket is listening...")

    # Clock Server Running forever
    while True:

       # Establish connection with client
       connection, address = s.accept()
       print('Server connected to', address)

       # Respond the client with server clock time
       connection.send(str(
                    datetime.datetime.now()).encode())

       # Close the connection with the client process
       connection.close()


# Driver function
if __name__ == '__main__':

    # Trigger the Clock Server
    initiateClockServer()

C#

using System;
using System.Net;
using System.Net.Sockets;
using System.Text;
using System.Threading;

class Program
{
    static void Main(string[] args)
    {
        // Trigger the Clock Server
        initiateClockServer();
    }

    static void initiateClockServer()
    {
        // Create socket
        Socket socketfd = new Socket(AddressFamily.InterNetwork, SocketType.Stream, ProtocolType.Tcp);
        Console.WriteLine("Socket successfully created");

        // Set port
        int port = 8000;

        // Bind socket to port
        IPEndPoint serverAddr = new IPEndPoint(IPAddress.Any, port);
        socketfd.Bind(serverAddr);
        Console.WriteLine("Socket is listening...");

        // Start listening to requests
        socketfd.Listen(5);

        // Clock Server Running forever
        while (true)
        {
            // Establish connection with client
            Socket clientSock = socketfd.Accept();
            Console.WriteLine("Server connected to " + clientSock.RemoteEndPoint.ToString());

            // Respond the client with server clock time
            DateTime now = DateTime.Now;
            string time_str = now.ToString();
            byte[] time_bytes = Encoding.ASCII.GetBytes(time_str);
            clientSock.Send(time_bytes);

            // Close the connection with the client process
            clientSock.Shutdown(SocketShutdown.Both);
            clientSock.Close();
        }
    }
}

Javascript

const net = require('net');
const port = 8000;

// function used to initiate the Clock Server
function initiateClockServer() {
    const server = net.createServer(function(connection) {
        console.log('Server connected to', connection.remoteAddress);

        // Respond the client with server clock time
        connection.write(new Date().toString());

        // Close the connection with the client process
        connection.end();
    });

    server.listen(port, function() {
        console.log("Socket is listening...");
    });
}

// Driver function
if (require.main === module) {
    // Trigger the Clock Server
    initiateClockServer();
}

// This code is contributed by rishab

Output:

Socket successfully created
Socket is listening...

Code below is used to initiate a prototype of a client process on the local machine:

Python3

# Python3 program imitating a client process

import socket
import datetime
from dateutil import parser
from timeit import default_timer as timer

# function used to Synchronize client process time
def synchronizeTime():

    s = socket.socket()

    # Server port
    port = 8000

    # connect to the clock server on local computer
    s.connect(('127.0.0.1', port))

    request_time = timer()

    # receive data from the server
    server_time = parser.parse(s.recv(1024).decode())
    response_time = timer()
    actual_time = datetime.datetime.now()

    print("Time returned by server: " + str(server_time))

    process_delay_latency = response_time - request_time

    print("Process Delay latency: " \
          + str(process_delay_latency) \
          + " seconds")

    print("Actual clock time at client side: " \
          + str(actual_time))

    # synchronize process client clock time
    client_time = server_time \
                      + datetime.timedelta(seconds = \
                               (process_delay_latency) / 2)

    print("Synchronized process client time: " \
                                        + str(client_time))

    # calculate synchronization error
    error = actual_time - client_time
    print("Synchronization error : "
                 + str(error.total_seconds()) + " seconds")

    s.close()


# Driver function
if __name__ == '__main__':

    # synchronize time using clock server
    synchronizeTime()

Output:

Time returned by server: 2018-11-07 17:56:43.302379
Process Delay latency: 0.0005150819997652434 seconds
Actual clock time at client side: 2018-11-07 17:56:43.302756
Synchronized process client time: 2018-11-07 17:56:43.302637
Synchronization error : 0.000119 seconds

Improvision in Clock Synchronization:
Using iterative testing over the network, we can define a minimum transfer time using which we can formulate an improved synchronization clock time(less synchronization error). 
Here, by defining a minimum transfer time, with a high confidence, we can say that the server time will 
always be generated after 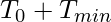and the 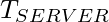will always be generated before 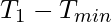, where 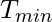is the minimum transfer time which is the minimum value of 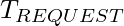and 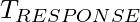during several iterative tests. Here synchronization error can be formulated as follows: 

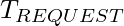
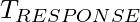
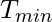
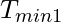
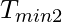
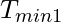
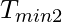
Similarly, if and differ by a considerable amount of time, we may substitute by and , where is the minimum observed request time and refers to the minimum observed response time over the network. 
The synchronized clock time in this case can be calculated as: 

So, by just introducing response and request time as separate time latencies, we can improve the synchronization of clock time and hence decrease the overall synchronization error. A number of iterative tests to be run depends on the overall clock drift observed.

Advantages:

Simple and easy to implement: Cristian’s Algorithm is a relatively simple algorithm and can be implemented easily on most computer systems.

Fast synchronization: The algorithm can synchronize the system clock with the time server quickly and efficiently.

Low network traffic: The algorithm requires only one round trip between the client and the server, which reduces network traffic and improves performance.

Works well for small networks: Cristian’s Algorithm works well for small networks where the network latency is relatively low.

Disadvantages:

Requires a trusted time server: Cristian’s Algorithm requires a trusted time server that provides accurate time information. If the time server is compromised or provides incorrect time information, it can lead to incorrect time synchronization.

Limited scalability: The algorithm is not suitable for large networks where the network latency can be high, as it may not be able to provide accurate time synchronization.

Not resilient to network failures: The algorithm does not handle network failures well, which can result in inaccurate time synchronization.

Vulnerable to malicious attacks: The algorithm is vulnerable to malicious attacks, such as man-in-the-middle attacks, which can lead to incorrect time synchronization.

References:
1) https://en.wikipedia.org/wiki/Cristian%27s_algorithm
2) https://en.wikipedia.org/wiki/Round-trip_delay_time
3) https://www.geeksforgeeks.org/socket-programming-python
4) https://en.wikipedia.org/wiki/Clock_drift