C++ Program to Find a triplet such that sum of two equals to third element

Write a C++ program for a given array of integers, you have to find three numbers such that the sum of two elements equals the third element.

Examples:

Input: {5, 32, 1, 7, 10, 50, 19, 21, 2}
Output: 21, 2, 19

Input: {5, 32, 1, 7, 10, 50, 19, 21, 0}
Output: no such triplet exist

Question source: Arcesium Interview Experience | Set 7 (On campus for Internship)

Simple approach:

Run three loops and check if there exists a triplet such that sum of two elements equals the third element.

Below is the implementation of the above approach:

C++

// CPP program to find three numbers
// such that sum of two makes the
// third element in array
#include <bits/stdc++.h>
using namespace std;

// Utility function for finding
// triplet in array
void findTriplet(int arr[], int n)
{
    for (int i = 0; i < n; i++) {
        for (int j = i + 1; j < n; j++) {
            for (int k = j + 1; k < n; k++) {
                if ((arr[i] + arr[j] == arr[k])
                    || (arr[i] + arr[k] == arr[j])
                    || (arr[j] + arr[k] == arr[i])) {
                    // printing out the first triplet
                    cout << "Numbers are: " << arr[i] << " "
                         << arr[j] << " " << arr[k];
                    return;
                }
            }
        }
    }

    // No such triplet is found in array
    cout << "No such triplet exists";
}

// driver program
int main()
{
    int arr[] = { 5, 32, 1, 7, 10, 50, 19, 21, 2 };
    int n = sizeof(arr) / sizeof(arr[0]);

    findTriplet(arr, n);
    return 0;
}

Output

Numbers are: 5 7 2

Time complexity: O(n^3)
Auxiliary Space: O(1)

Efficient approach:

The idea is similar to Find a triplet that sum to a given value.

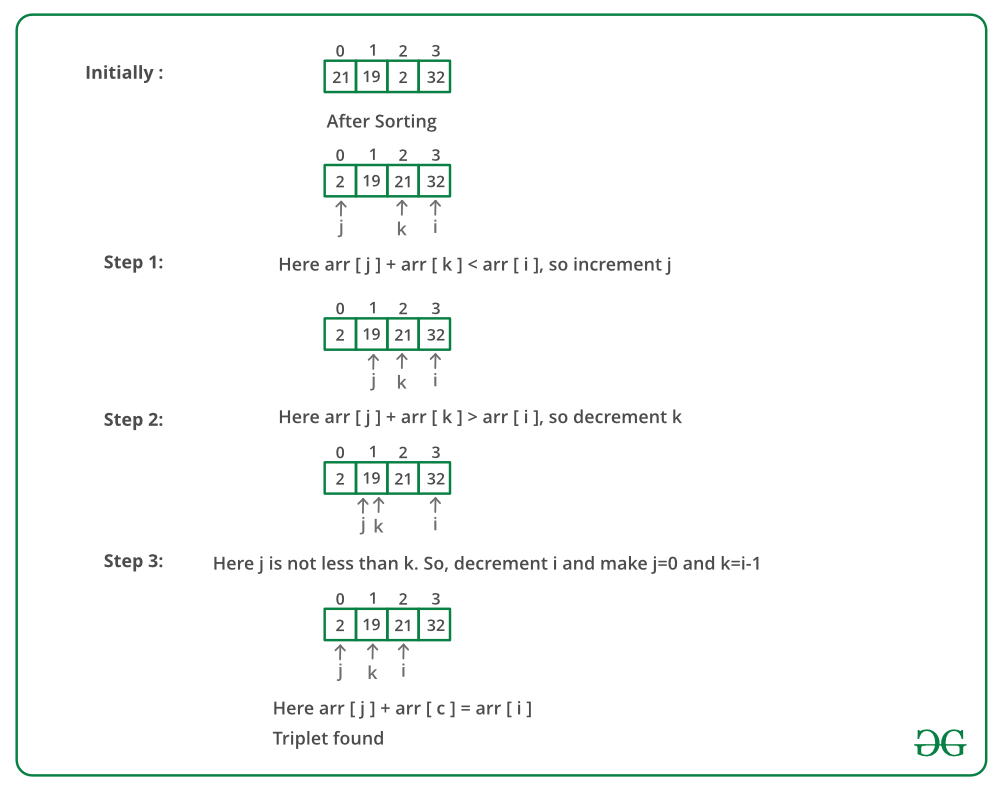
Step-by-step approach:

• Sort the given array first.
• Start fixing the greatest element of three from the back and traverse the array to find the other two numbers which sum up to the third element.
• Take two pointers j(from front) and k(initially i-1) to find the smallest of the two number and from i-1 to find the largest of the two remaining numbers
• If the addition of both the numbers is still less than A[i], then we need to increase the value of the summation of two numbers, thereby increasing the j pointer, so as to increase the value of A[j] + A[k].
• If the addition of both the numbers is more than A[i], then we need to decrease the value of the summation of two numbers, thereby decrease the k pointer so as to decrease the overall value of A[j] + A[k].

Below image is a dry run of the above approach:

Below is the implementation of the above approach:

C++

// C++ program to find three numbers
// such that sum of two makes the
// third element in array
#include <bits/stdc++.h>
using namespace std;

// Utility function for finding
// triplet in array
void findTriplet(int arr[], int n)
{
    // Sort the array
    sort(arr, arr + n);

    // For every element in arr check
    // if a pair exist(in array) whose
    // sum is equal to arr element
    for (int i = n - 1; i >= 0; i--)
    {
        int j = 0;
        int k = i - 1;

        // Iterate forward and backward to
        // find the other two elements
        while (j < k)
        {
            // If the two elements sum is
            // equal to the third element
            if (arr[i] == arr[j] + arr[k])
            {
                // Pair found
                cout << "numbers are " << arr[i] <<
                        " " << arr[j] << " " <<
                        arr[k] << endl;
                return;
            }

            // If the element is greater than
            // sum of both the elements, then try
            // adding a smaller number to reach the
            // equality
            else if (arr[i] > arr[j] + arr[k])
                j += 1;

            // If the element is smaller, then
            // try with a smaller number
            // to reach equality, so decrease K
            else
                k -= 1;
        }
    }

    // No such triplet is found in array
    cout << "No such triplet exists";
}

// Driver code
int main()
{
    int arr[] = {5, 32, 1, 7, 10,
                 50, 19, 21, 2};
    int n = sizeof(arr) / sizeof(arr[0]);
    findTriplet(arr, n);
    return 0;
}

Output:

numbers are 21 2 19

Time complexity: O(N^2)
Auxiliary Space: O(1)

C++ Program to Find a triplet such that sum of two equals to third element using Binary Search.

1. Sort the given array.
2. Start a nested loop, fixing the first element i(from 0 to n-1) and moving the other one j (from i+1 to n-1).
3. Take the sum of both the elements and search it in the remaining array using Binary Search.

Below is the implementation of the above approach:

C++

// C++ program to find three numbers
// such that sum of two makes the
// third element in array
#include <bits/stdc++.h>
#include <iostream>
using namespace std;

// Function to perform binary search
bool search(int sum, int start,
            int end, int arr[])
{
    while (start <= end)
    {
        int mid = (start + end) / 2;
        if (arr[mid] == sum)
        {
            return true;
        }
        else if (arr[mid] > sum)
        {
            end = mid - 1;
        }
        else
        {
            start = mid + 1;
        }
    }
    return false;
}

// Function to find the triplets
void findTriplet(int arr[], int n)
{
    // Sorting the array
    sort(arr, arr + n);

    // Initialising nested loops
    for (int i = 0; i < n; i++)
    {
        for (int j = i + 1; j < n; j++)
        {
            // Finding the sum of the numbers
            if (search((arr[i] + arr[j]),
                j, n - 1, arr))
            {
                // Printing out the first triplet
                cout << "Numbers are: " << arr[i] <<
                        " " << arr[j] << " " <<
                        (arr[i] + arr[j]);
                return;
            }
        }
    }
    // If no such triplets are found
    cout << "No such numbers exist" << endl;
}

// Driver code
int main()
{
    int arr[] = {5, 32, 1, 7, 10,
                 50, 19, 21, 2};
    int n = sizeof(arr) / sizeof(arr[0]);
    findTriplet(arr, n);
    return 0;
}
// This code is contributed by Sarthak Delori

Time Complexity: O(N^2*log N)
Auxiliary Space: O(1)

Please refer complete article on Find a triplet such that sum of two equals to third element for more details!