Counting Boolean function with some variables

Prerequisite – Canonical and Standard Form
In the below articles, we will see some varieties of problems with three variables.

Statement-1:
Counting the number of Boolean functions possible with two variables such that there are exactly two min terms.

Explanation:
As we already know that from two variables (a and b) four $(2^2)$ numbers (0, 1, 2, 3) can be formed i.e, in binary digits 00, 01, 10, 11 and possible Min terms are a’b’, a’b, ab’, ab respectively which gives ‘1’ as the output for respective binary digits as input.

Thus the number of possible function with two variables as input such that there are exactly two min terms are,
```
 
```
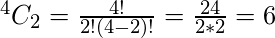
Where ‘4’ is the possible number from two variables and ‘2’ is the desired number of min terms for which the number of the function needs to be calculated.
Statement-2:
Counting the number of Boolean functions possible with three variables such that there are exactly three min terms.

Explanation:
As we already know that from three variables (a, b and c), 8 $(2^3)$ numbers (0, 1, 2, 3, 4, 5, 6, 7) can be formed i.e, in binary digits 000, 001, 010, 011, 100, 101, 110, 111 and possible Min terms are a’b’c’, a’b’c, a’bc’, a’bc, ab’c, abc’, abc respectively which gives ‘1’ as the output for respective binary digits as input.

Thus the number of possible function with three variables as input such that there are exactly three min terms are,
```
 
```
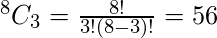
Where ‘8’ is the possible number from three variables and ‘3’ is the desired number of min terms for which the number of the function need to be calculated.
Statement-3:
Counting the number of boolean functions possible with three variables such that there are atmost 4 min terms.

Explanation:
As we already know that from three variables (a, b and c), 8 $(2^3)$ numbers (0, 1, 2, 3, 4, 5, 6, 7) can be formed, i.e., in binary digits 000, 001, 010, 011, 100, 101, 110, 111 and possible Min terms are a’b’c’, a’b’c, a’bc’, a’bc, ab’c, abc’, abc respectively which gives ‘1’ as the output for respective binary digits as input.
Thus the number of possible function with three variables as input such that there are at most 4 min terms are,
```
 
```
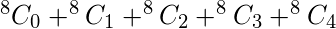
Where ‘8’ is the possible number from three variables and 0, 1, 2, 3, 4 are the desired number of min terms for which the number of the function need to be calculated.
Statement-4:
Counting the number of Boolean functions possible with three variables such that there are minimum 4 min terms.

Explanation:
As we already know that from three variables (a, b and c), 8 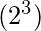$(2^3)$ numbers (0, 1, 2, 3, 4, 5, 6, 7) can be formed i.e, in binary digits 000, 001, 010, 011, 100, 101, 110, 111 and possible Min terms are a’b’c’, a’b’c, a’bc’, a’bc, ab’c, abc’, abc respectively which gives ‘1’ as the output for respective binary digits as input.
Thus the number of possible function with three variables as input such that there are minimum 4 min terms are,
```
 
```
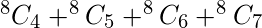
Where ‘8’ is the possible number from three variables and 4, 5, 6, 7 are the desired number of min terms for which the number of the function need to be calculated.
Statement-5:
Counting the number of Boolean functions possible with ‘k’ variables such that there are ‘m’ min terms.

Explanation:
As we already know that from ‘k’ variables, 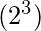$(2^3)$ numbers can be formed.
Thus the number of possible function with ‘k’ variables as input such that there are ‘m’ min terms are,
```
 
```
Where 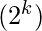$(2^k)$ is the possible number from ‘k’ variables and ‘m’ are the desired number of min terms for which the number of the function need to be calculated.
Statement-6:
Counting the number of Boolean functions possible in neutral function of ‘3’ variables where there is equal number of min and max terms.

Explanation:
As we already know that from three variables (a, b and c), 8 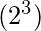$(2^3)$ numbers (0, 1, 2, 3, 4, 5, 6, 7) can be formed i.e, in binary digits 000, 001, 010, 011, 100, 101, 110, 111 and there are equal number of max and min terms which gives ‘1’ as the output for min terms and ‘0’ as the output for max terms for respective binary digits as input.

For example, suppose 000 is the binary digits then min terms will be a’b’c’ and max terms will be abc.
Thus the number of possible Boolean function with three variables in the neutral function are,
```
 
```
Where ‘8’ is the possible number from three variables and 4 are the desired number of min terms or max terms for which the number of the function needs to be calculated.
Statement-7:
Counting the number of Boolean functions possible in neutral function of ‘k’ variables where there is an equal number of min and max terms.

Explanation:
As we already know that from ‘k’ variables, 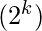$(2^k)$ numbers can be formed.
Thus the number of possible Boolean function with ‘k’ variables as input where an equal number of min and max terms are,
```
 
```
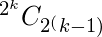
Where 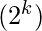$(2^k)$ is the possible number from ‘k’ variables and 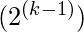$(2^{(k-1)})$ are the desired number of either min or max terms for which the number of the function needs to be calculated.

My Personal Notes

Recommended Posts: