Count ways to distribute m items among n people

Given m and n representing number of mangoes and number of people respectively. Task is to calculate number of ways to distribute m mangoes among n people. Considering both variables m and n, we arrive at 4 typical use cases where mangoes and people are considered to be:
1) Both identical 
2) Unique and identical respectively 
3) Identical and unique respectively 
4) Both unique 
Prerequisites: Binomial Coefficient | Permutation and Combination

Case 1: Distributing m identical mangoes amongst n identical people
If we try to spread m mangoes in a row, our goal is to divide these m mangoes among n people sitting somewhere between arrangement of these mangoes. All we need to do is pool these m mangoes into n sets so that each of these n sets can be allocated to n people respectively. 
To accomplish above task, we need to partition the initial arrangement of mangoes by using n-1 partitioners to create n sets of mangoes. In this case we need to arrange m mangoes and n-1 partitioners all together. So we need 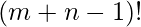ways to calculate our answer. 
Illustration given below represents an example(a way) of an arrangement of partitions created after placing 3 partitioners namely P1, P2, P3 which partitioned all 7 mangoes into 4 different partitions so that 4 people can have their own portion of respective partition: 

As all the mangoes are considered to be identical, we divide 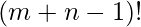by 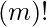to deduct the duplicate entries. Similarly, we divide the above expression again by because all people are considered to be identical too.
The final expression we get is :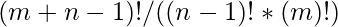 
The above expression is even-actually equal to the binomial coefficient: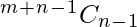 
Example: 

Input :  m = 3, n = 2
Output : 4
There are four ways
3 + 0, 1 + 2, 2 + 1 and 0 + 3 

Input :  m = 13, n = 6
Output : 8568

Input :  m = 11, n = 3
Output : 78

C++

// C++ code for calculating number of ways
// to distribute m mangoes amongst n people
// where all mangoes and people are identical
#include <bits/stdc++.h>
using namespace std;

// function used to generate binomial coefficient
// time complexity O(m)
int binomial_coefficient(int n, int m)
{
    int res = 1;

    if (m > n - m)
        m = n - m;

    for (int i = 0; i < m; ++i) {
        res *= (n - i);
        res /= (i + 1);
    }

    return res;
}

// helper function for generating no of ways
// to distribute m mangoes amongst n people
int calculate_ways(int m, int n)
{
    // not enough mangoes to be distributed
    if (m < n)
        return 0;

    // ways  -> (n+m-1)C(n-1)
    int ways = binomial_coefficient(n + m - 1, n - 1);
    return ways;
}

// Driver function
int main()
{
    // m represents number of mangoes
    // n represents number of people
    int m = 7, n = 5;

    int result = calculate_ways(m, n);
    printf("%d\n", result);

    return 0;
}

Java

// Java code for calculating number of ways
// to distribute m mangoes amongst n people
// where all mangoes and people are identical

import java.util.*;

class GFG {

    // function used to generate binomial coefficient
    // time complexity O(m)
    public static int binomial_coefficient(int n, int m)
    {
        int res = 1;

        if (m > n - m)
            m = n - m;

        for (int i = 0; i < m; ++i) {
            res *= (n - i);
            res /= (i + 1);
        }

        return res;
    }

    // helper function for generating no of ways
    // to distribute m mangoes amongst n people
    public static int calculate_ways(int m, int n)
    {

        // not enough mangoes to be distributed
        if (m < n) {
            return 0;
        }

        // ways  -> (n+m-1)C(n-1)
        int ways = binomial_coefficient(n + m - 1, n - 1);
        return ways;
    }

    // Driver function
    public static void main(String[] args)
    {

        // m represents number of mangoes
        // n represents number of people
        int m = 7, n = 5;

        int result = calculate_ways(m, n);
        System.out.println(Integer.toString(result));

        System.exit(0);
    }
}

Python3

# Python code for calculating number of ways
# to distribute m mangoes amongst n people
# where all mangoes and people are identical


# function used to generate binomial coefficient
# time complexity O(m)
def binomial_coefficient(n, m):
    res = 1

    if m > n - m:
        m = n - m

    for i in range(0, m):
        res *= (n - i)
        res /= (i + 1)

    return res

# helper function for generating no of ways
# to distribute m mangoes amongst n people
def calculate_ways(m, n):

    # not enough mangoes to be distributed
    if m<n:
        return 0

    # ways  -> (n + m-1)C(n-1)
    ways = binomial_coefficient(n + m-1, n-1)
    return int(ways)

# Driver function
if __name__ == '__main__':

    # m represents number of mangoes
    # n represents number of people
    m = 7 ;n = 5

    result = calculate_ways(m, n)
    print(result)

C#

// C# code for calculating number
// of ways to distribute m mangoes
// amongst n people where all mangoes
// and people are identical
using System;

class GFG
{

// function used to generate
// binomial coefficient
// time complexity O(m)
public static int binomial_coefficient(int n,
                                       int m)
{
    int res = 1;

    if (m > n - m)
        m = n - m;

    for (int i = 0; i < m; ++i)
    {
        res *= (n - i);
        res /= (i + 1);
    }

    return res;
}

// helper function for generating
// no of ways to distribute m
// mangoes amongst n people
public static int calculate_ways(int m, int n)
{

    // not enough mangoes
    // to be distributed
    if (m < n)
    {
        return 0;
    }

    // ways -> (n+m-1)C(n-1)
    int ways = binomial_coefficient(n + m - 1,
                                    n - 1);
    return ways;
}

// Driver Code
public static void Main()
{

    // m represents number of mangoes
    // n represents number of people
    int m = 7, n = 5;

    int result = calculate_ways(m, n);
    Console.WriteLine(result.ToString());
}
}

// This code is contributed
// by Subhadeep

PHP

<?php
// PHP code for calculating number
// of ways to distribute m mangoes
// amongst n people where all
// mangoes and people are identical

// function used to generate
// binomial coefficient
// time complexity O(m)
function binomial_coefficient($n, $m)
{
    $res = 1;

    if ($m > $n - $m)
        $m = $n - $m;

    for ($i = 0; $i < $m; ++$i)
    {
        $res *= ($n - $i);
        $res /= ($i + 1);
    }

    return $res;
}

// Helper function for generating
// no of ways to distribute m.
// mangoes amongst n people
function calculate_ways($m, $n)
{
    // not enough mangoes to
    // be distributed
    if ($m < $n)
        return 0;

    // ways -> (n+m-1)C(n-1)
    $ways = binomial_coefficient($n + $m - 1,
                                      $n - 1);
    return $ways;
}

// Driver Code

// m represents number of mangoes
// n represents number of people
$m = 7;
$n = 5;

$result = calculate_ways($m, $n);
echo $result;

// This code is contributed
// by Shivi_Aggarwal
?>

Javascript

<script>

// Javascript code for calculating number of ways
// to distribute m mangoes amongst n people
// where all mangoes and people are identical

// function used to generate binomial coefficient
// time complexity O(m)
function binomial_coefficient(n, m)
{
    let res = 1;

    if (m > n - m)
        m = n - m;

    for (let i = 0; i < m; ++i) {
        res *= (n - i);
        res /= (i + 1);
    }

    return res;
}

// helper function for generating no of ways
// to distribute m mangoes amongst n people
function calculate_ways(m, n)
{
    // not enough mangoes to be distributed
    if (m < n)
        return 0;

    // ways -> (n+m-1)C(n-1)
    let ways = binomial_coefficient(n + m - 1, n - 1);
    return ways;
}

// Driver function

    // m represents number of mangoes
    // n represents number of people
    let m = 7, n = 5;

    let result = calculate_ways(m, n);
    document.write(result);

// This code is contributed by Mayank Tyagi
</script>

Output:

330

Time Complexity : O(n) 
Auxiliary Space : O(1)
Case 2: Distributing m unique mangoes amongst n identical people
In this case, to calculate the number of ways to distribute m unique mangoes amongst n identical people, we just need to multiply the last expression 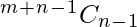we calculated in Case 1 by . 
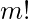So our final expression for this case is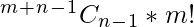 
Proof:
In case 1, initially we got the expression 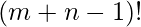without removing duplicate entries. 
In this case, we only need to divide as all mangoes are considered to be unique in this case. 
So we get the expression as :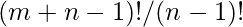 
Multiplying both numerator and denominator by , 
we get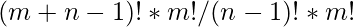 
Where ===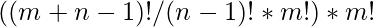 
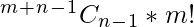
Time Complexity : O(max(n, m)) 
Auxiliary Space : O(1)
Case 3: Distributing m identical mangoes amongst n unique people
In this case, to calculate the number of ways to distribute m identical mangoes amongst n unique people, we just need to multiply the last expression 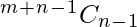we calculated in Case 1 by . 
So our final expression for this case is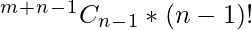 
Proof:
This Proof is pretty much similar to the proof of last case expression. 
In case 1, initially we got the expression 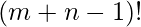without removing duplicate entries. 
In this case, we only need to divide 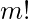as all people are considered to be unique in this case. 
So we get the expression as :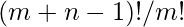 
Multiplying both numerator and denominator by , 
we get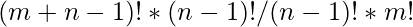 
Where === 
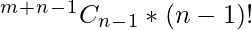
Time Complexity : O(n) 
Auxiliary Space : O(1)
For references on how to calculate 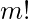refer here factorial of a number
Case 4: Distributing m unique mangoes amongst n unique people
In this case we need to multiply the expression obtained in case 1 by both 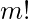and . 
The proofs for both of the multiplications are defined in case 2 and case 3.
Hence, in this case, our final expression comes out to be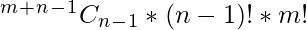 
Time Complexity : O(n+m) 
Auxiliary Space : O(1)