Count unordered pairs (i,j) such that product of a[i] and a[j] is power of two
Last Updated :
06 Sep, 2022
Given an array of N elements. The task is to count unordered pairs (i, j) in the array such that the product of a[i] and a[j] can be expressed as a power of two.
Examples:
Input : arr[] = {2, 3, 4, 8, 10}
Output : 3
Explanation: The pair of array element will be
(2, 4), (2, 8), (4, 8) whose product are
8, 16, 32 respectively which can be expressed
as power of 2, like 2^3, 2^4, 2^5.
Input : arr[] = { 2, 5, 8, 16, 128 }
Output : 6
If you multiply 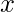 and
and 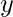 and their product become
and their product become 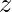 , then z=x*y, now if it’s possible to express
, then z=x*y, now if it’s possible to express 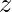 as power of two then it can be proved that both
as power of two then it can be proved that both 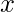 and
and 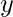 can be expressed as power of two. Basically z= 2a = 2(b+c) = 2b * 2c = x * y, where
can be expressed as power of two. Basically z= 2a = 2(b+c) = 2b * 2c = x * y, where 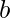 and
and 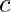 both can hold a minimum value 0.
both can hold a minimum value 0.
So now we have to count the number of elements in the array which can be expressed as a power of two. If the count is k, then answer will be kC2 = k*(k-1)/2, as we need the count of unordered pairs.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool isPowerOfTwo(int x)
{
return x && (!(x&(x-1)));
}
void Count_pairs(int a[], int n)
{
int count = 0;
for (int i = 0; i < n; i++) {
if (isPowerOfTwo(a[i]))
count++;
}
int ans = (count * (count - 1)) / 2;
cout << ans << "\n";
}
int main()
{
int a[] = { 2, 5, 8, 16, 128 };
int n = sizeof(a) / sizeof(a[0]);
Count_pairs(a, n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static boolean isPowerOfTwo(int x)
{
return (x >0&& (!((x&(x-1))>0)));
}
static void Count_pairs(int a[], int n)
{
int count = 0;
for (int i = 0; i < n; i++) {
if (isPowerOfTwo(a[i]))
count++;
}
int ans = (count * (count - 1)) / 2;
System.out.println( ans);
}
public static void main (String[] args) {
int a[] = { 2, 5, 8, 16, 128 };
int n = a.length;
Count_pairs(a, n);
}
}
|
Python 3
def isPowerOfTwo(x) :
return (x and(not(x & (x - 1))))
def Count_pairs(a, n) :
count = 0
for i in range(n) :
if isPowerOfTwo(a[i]) :
count += 1
ans = (count * (count - 1)) / 2
print(ans)
if __name__ == "__main__" :
a = [ 2, 5, 8, 16, 128]
n = len(a)
Count_pairs(a, n)
|
C#
using System;
public class GFG{
static bool isPowerOfTwo(int x)
{
return (x >0&& (!((x&(x-1))>0)));
}
static void Count_pairs(int []a, int n)
{
int count = 0;
for (int i = 0; i < n; i++) {
if (isPowerOfTwo(a[i]))
count++;
}
int ans = (count * (count - 1)) / 2;
Console.WriteLine( ans);
}
static public void Main (){
int []a = { 2, 5, 8, 16, 128 };
int n = a.Length;
Count_pairs(a, n);
}
}
|
PHP
<?php
function isPowerOfTwo($x)
{
return ($x && (!($x & ($x - 1))));
}
function Count_pairs($a, $n)
{
$count = 0;
for ($i = 0; $i < $n; $i++)
{
if (isPowerOfTwo($a[$i]))
$count++;
}
$ans = ($count * ($count - 1)) / 2;
echo $ans , "\n";
}
$a = array( 2, 5, 8, 16, 128 );
$n = sizeof($a);
Count_pairs($a, $n);
?>
|
Javascript
<script>
function isPowerOfTwo( x)
{
return (x >0&& (!((x&(x-1))>0)));
}
function Count_pairs(a,n)
{
let count = 0;
for (let i = 0; i < n; i++) {
if (isPowerOfTwo(a[i]))
count++;
}
let ans = (count * (count - 1)) / 2;
document.write( ans);
}
let a = [ 2, 5, 8, 16, 128 ];
let n = a.length;
Count_pairs(a, n);
</script>
|
Complexity Analysis:
- Time Complexity: O(N), where N is the number of elements in the array.
- Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...