Count triplets from a given range having sum of two numbers of a triplet equal to the third number
Last Updated :
31 Mar, 2023
Given two integers L and R, the task is to find the number of unique triplets whose values lie in the range [L, R], such that the sum of any two numbers is equal to the third number.
Examples:
Input: L = 1, R = 3
Output: 3
Explanation: Three such triplets satisfying the necessary conditions are (1, 1, 2), (1, 2, 3) and (2, 1, 3).
Input: L = 2, R = 6
Output: 6
Naive Approach: The simplest approach to solve the problem is to generate all possible triplets over the range [L, R] and count those triplets having sum of any two numbers from the pair equal to the third number. After checking for all the triplets, print the total count obtained.
C++
#include <bits/stdc++.h>
using namespace std;
int totalCombination(int L, int R)
{
int count=0;
for(int i=L;i<=R;i++){
for(int j=L;j<=R;j++){
for(int k=L;k<=R;k++){
if(i+j==k){
count++;}
}
}
}
return count;
}
int main()
{
int L = 1, R = 3;
cout << totalCombination(L, R);
return 0;
}
|
Java
import java.util.*;
public class Main {
public static int totalCombination(int L, int R) {
int count = 0;
for (int i = L; i <= R; i++) {
for (int j = L; j <= R; j++) {
for (int k = L; k <= R; k++) {
if (i + j == k) {
count++;
}
}
}
}
return count;
}
public static void main(String[] args) {
int L = 1, R = 3;
System.out.println(totalCombination(L, R));
}
}
|
Python3
def total_combination(L, R):
count = 0
for i in range(L, R+1):
for j in range(L, R+1):
for k in range(L, R+1):
if i + j == k:
count += 1
return count
L = 1
R = 3
print(total_combination(L, R))
|
Javascript
function totalCombination(L, R) {
let count = 0;
for (let i = L; i <= R; i++) {
for (let j = L; j <= R; j++) {
for (let k = L; k <= R; k++) {
if (i + j == k) {
count++;
}
}
}
}
return count;
}
let L = 1,
R = 3;
console.log(totalCombination(L, R));
|
C#
using System;
class GFG {
static int totalCombination(int L, int R)
{
int count = 0;
for (int i = L; i <= R;
i++) {
for (int j = L; j <= R; j++) {
for (int k = L; k <= R; k++) {
if (i + j == k) {
count++;
}
}
}
}
return count;
}
static void Main()
{
int L = 1, R = 3;
Console.WriteLine(totalCombination(L, R));
}
}
|
Time Complexity: O((R – L)3)
Auxiliary Space: O(1)
Efficient Approach: The above approach can be optimized based on the following observations:
- If the difference between the given range is less than L, then there doesn’t exist any such triplet having the sum of two numbers equal to the third number.
- If the difference between the given range is at least L, then (R – L) lies in the range L and R, i.e. {L, (R – L), R}. It can be observed that the sum of L and any other number in the range [L, R – L] is at most R.
- Therefore, the total number of possible valid triplets, where the first element is L is given by (R – L – L + 1).
- Similarly, when the first element is (L + 1), then the number of triplets is (R – L – L), and so on.
From the above observations, the total number of triplets forms an AP with the terms (R – L – L + 1), (R – L – L), (R – L – L – 1), ……… consisting of (R – L – L + 1) number of terms. Therefore, the total number of triplets is given by:
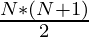
where, N is (R – L – L + 1)
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int totalCombination(int L, int R)
{
int count = 0;
int K = R - L;
if (K < L)
return 0;
int ans = K - L;
count = ((ans + 1) * (ans + 2)) / 2;
return count;
}
int main()
{
int L = 2, R = 6;
cout << totalCombination(L, R);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int totalCombination(int L, int R)
{
int count = 0;
int K = R - L;
if (K < L)
return 0;
int ans = K - L;
count = ((ans + 1) * (ans + 2)) / 2;
return count;
}
public static void main(String[] args)
{
int L = 2, R = 6;
System.out.print(totalCombination(L, R));
}
}
|
Python3
def totalCombination(L, R):
count = 0
K = R - L
if (K < L):
return 0
ans = K - L
count = ((ans + 1) * (ans + 2)) // 2
return count
if __name__ == '__main__':
L, R = 2, 6
print (totalCombination(L, R))
|
C#
using System;
class GFG
{
static int totalCombination(int L, int R)
{
int count = 0;
int K = R - L;
if (K < L)
return 0;
int ans = K - L;
count = ((ans + 1) * (ans + 2)) / 2;
return count;
}
public static void Main()
{
int L = 2, R = 6;
Console.WriteLine(totalCombination(L, R));
}
}
|
Javascript
<script>
function totalCombination(L, R)
{
let count = 0;
let K = R - L;
if (K < L)
return 0;
let ans = K - L;
count = ((ans + 1) * (ans + 2)) / 2;
return count;
}
let L = 2, R = 6;
document.write(totalCombination(L, R));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...