Count the number of intervals in which a given value lies

Given a 2D-array of 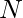integer intervals and a value 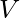. For every interval [l_i, r_i], the task is to check if V lies in between li and ri, both inclusive. The task is to print the count of intervals that satisfies this. 
Note: 1<=l_i<= r_i
Examples:

Input: arr[][] = {{1, 10}, {5, 10}, {15, 25}, {7, 12}, {20, 25}}, V = 7 
Output: 3 
For V = 7, it lies in the intervals [1, 10], [5, 10] and [7, 12]. So, the count of intervals V lies in is 3.
Input: arr[][] = {{3, 7}, {2, 2}, {2, 8}, {7, 11}}, V = 2 
Output: 2 
For V = 2, it lies in the intervals [2, 2] and [2, 8]. So, the count of intervals V lies in is 2. 

Method-1: Traverse the entire array checking for every interval [li, ri], if V lies in the interval or not. If it does, then increment the count.
Below is the implementation of the above approach: 

C++

// CPP program to count the
// number of intervals in which
// a given value lies

#include<bits/stdc++.h>
using namespace std;

    // Function to count the
    // number of intervals in which
    // a given value lies
    int countIntervals(int arr[][2], int V, int N)
    {
        // Variable to store the count of intervals
        int count = 0;

        // Variables to store start and end of an interval
        int li, ri;

        for (int i = 0; i < N; i++)
       {
            li = arr[i][0];
            ri = arr[i][1];

            // Implies V lies in the interval
            // so increase count
            if (V >= li && V <= ri)
                count++;
        }
        return count;
    }

    // Driver code
    int main()
    {
        int arr[][2] = { { 1, 10 }, { 5, 10 },{ 15, 25 }, { 7, 12 }, { 20, 25 } };

        int V = 7;

        // length of the array
        int N = sizeof(arr)/sizeof(arr[0]);
        cout<<(countIntervals(arr, V, N))<<endl;
    }
//This code is contributed by
// Surendra_Gangywar

Java

// Java program to count the
// number of intervals in which
// a given value lies

import java.io.*;
import java.util.*;
import java.lang.*;

class GFG {

    // Function to count the
    // number of intervals in which
    // a given value lies
    static int countIntervals(int[][] arr, int V, int N)
    {
        // Variable to store the count of intervals
        int count = 0;

        // Variables to store start and end of an interval
        int li, ri;

        for (int i = 0; i < N; i++) {
            li = arr[i][0];
            ri = arr[i][1];

            // Implies V lies in the interval
            // so increase count
            if (V >= li && V <= ri)
                count++;
        }
        return count;
    }

    // Driver code
    public static void main(String args[])
    {
        int[][] arr = { { 1, 10 }, { 5, 10 },
         { 15, 25 }, { 7, 12 }, { 20, 25 } };

        int V = 7;

        // length of the array
        int N = arr.length;

        System.out.println(countIntervals(arr, V, N));
    }
}

Python3

# Python 3 program to count the
# number of intervals in which
# a given value lies

# Function to count the
# number of intervals in which
# a given value lies
def countIntervals(arr, V, N) :

    # Variable to store the
    # count of intervals
    count = 0

    # Variables to store start and
    # end of an interval
    for i in range(N) :

        # Variables to store start and
        # end of an interval
        li = arr[i][0]
        ri = arr[i][1]

        # Implies V lies in the interval
        # so increase count
        if (V >= li and V <= ri) :
            count += 1

    return count;

# Driver Code
if __name__ == "__main__" :

    arr = [ [ 1, 10 ], [ 5, 10 ],
            [ 15, 25 ], [ 7, 12 ],
            [ 20, 25 ] ]

    V = 7

    # length of the array
    N = len(arr)

    print((countIntervals(arr, V, N)))

# This code is contributed by Ryuga

C#

// C# program to count the
// number of intervals in which
// a given value lies
using System;

class GFG
{

// Function to count the
// number of intervals in which
// a given value lies
static int countIntervals(int[,] arr, int V, int N)
{
    // Variable to store the count of intervals
    int count = 0;

    // Variables to store start and end of an interval
    int li, ri;

    for (int i = 0; i < N ; i++)
    {
        li = arr[i, 0];
        ri = arr[i, 1];

        // Implies V lies in the interval
        // so increase count
        if (V >= li && V <= ri)
            count++;
    }
    return count;
}

// Driver code
public static void Main()
{
    int[,] arr = new int[,]{ { 1, 10 }, { 5, 10 },
    { 15, 25 }, { 7, 12 }, { 20, 25 } };

    int V = 7;

    // length of the array
    int N = arr.GetLength(0);

    Console.WriteLine(countIntervals(arr, V, N));
}
}

// This code is contributed by Akanksha Rai

PHP

<?php
// PHP program to count the number of
// intervals in which a given value lies

// Function to count the number of
// intervals in which a given value lies
function countIntervals($arr, $V, $N)
{
    // Variable to store the
    // count of intervals
    $count = 0;

    // Variables to store start
    // and end of an interval
    for ($i = 0; $i < $N; $i++)
    {
        $li = $arr[$i][0];
        $ri = $arr[$i][1];

        // Implies V lies in the interval
        // so increase count
        if ($V >= $li && $V <= $ri)
            $count++;
    }
    return $count;
}

// Driver code
$arr = array(array(1, 10),
             array(5, 10),
             array(15, 25),
             array(7, 12),
             array(20, 25));

$V = 7;

// length of the array
$N = sizeof($arr);

echo countIntervals($arr, $V, $N);

// This code is contributed
// by Akanksha Rai
?>

Javascript

<script>
    // Javascript program to count the
    // number of intervals in which
    // a given value lies

    // Function to count the
    // number of intervals in which
    // a given value lies
    function countIntervals(arr, V, N)
    {

        // Variable to store the count of intervals
        let count = 0;

        // Variables to store start and end of an interval
        let li, ri;

        for (let i = 0; i < N; i++) {
            li = arr[i][0];
            ri = arr[i][1];

            // Implies V lies in the interval
            // so increase count
            if (V >= li && V <= ri)
                count++;
        }
        return count;
    }

    let arr = [ [ 1, 10 ], [ 5, 10 ],
                 [ 15, 25 ], [ 7, 12 ], [ 20, 25 ] ];

    let V = 7;

    // length of the array
    let N = arr.length;

    document.write(countIntervals(arr, V, N));

    // This code is contributed by decode2207.
</script>

Output:

3

Time Complexity: O(N)

Auxiliary Space: O(1)

Method-2(Efficient for queries): Use a frequency array that keeps track of how many of the given intervals an element lies in. 

1. For every interval [L, R], put freq[L] as freq[L] + 1 and freq[R+1] as freq[R + 1] – 1 indicating start and end of the interval.
2. Keep track of the overall minimum and maximum of the intervals.
3. Starting from minimum to maximum construct the frequency array from its previous element i.e., 
   freq[i] = freq[i] + freq[i – 1].
4. Required count of intervals is then given by freq[V].

Below is the implementation of the above approach: 

C++

// C++ program to count the
// number of intervals in which
// a given value lies
#include<bits/stdc++.h>
using namespace std;

const int MAX_VAL = 200000;

// Function to count the
// number of intervals in which
// a given value lies
int countIntervals(int arr[][2], int V, int N)
{
    // Variables to store overall minimum and
    // maximum of the intervals
    int min = INT_MAX;
    int max = INT_MIN;

    // Variables to store start and
    // end of an interval
    int li, ri;

    // Frequency array to keep track of
    // how many of the given intervals
    // an element lies in
    int freq[MAX_VAL];

    for (int i = 0; i < N; i++)
    {
        li = arr[i][0];
        freq[li] = freq[li] + 1;
        ri = arr[i][1];
        freq[ri + 1] = freq[ri + 1] - 1;

        if (li < min)
            min = li;
        if (ri > max)
            max = ri;
    }

    // Constructing the frequency array
    for (int i = min; i <= max; i++)
        freq[i] = freq[i] + freq[i - 1];

    return freq[V];
}

// Driver code
int main()
{
    int arr[5][2] = { { 1, 10 }, { 5, 10 },
                      { 15, 25 }, { 7, 12 },
                      { 20, 25 } };

    int V = 7;

    // length of the array
    int N = sizeof(arr) / sizeof(arr[0]);

    cout << (countIntervals(arr, V, N));
}

// This code is contributed by
// Surendra_Gangwar

Java

// Java program to count the
// number of intervals in which
// a given value lies

import java.io.*;
import java.util.*;
import java.lang.*;

class GFG {

    static final int MAX_VAL = 200000;

    // Function to count the
    // number of intervals in which
    // a given value lies
    static int countIntervals(int[][] arr, int V, int N)
    {
        // Variables to store overall minimum and
        // maximum of the intervals
        int min = Integer.MAX_VALUE, max = Integer.MIN_VALUE;

        // Variables to store start and end of an interval
        int li, ri;

        // Frequency array to keep track of
        // how many of the given intervals an element lies in
        int[] freq = new int[MAX_VAL];

        for (int i = 0; i < N; i++) {
            li = arr[i][0];
            freq[li] = freq[li] + 1;
            ri = arr[i][1];
            freq[ri + 1] = freq[ri + 1] - 1;

            if (li < min)
                min = li;
            if (ri > max)
                max = ri;
        }

        // Constructing the frequency array
        for (int i = min; i <= max; i++)
            freq[i] = freq[i] + freq[i - 1];

        return freq[V];
    }

    // Driver code
    public static void main(String args[])
    {
        int[][] arr = { { 1, 10 }, { 5, 10 },
         { 15, 25 }, { 7, 12 }, { 20, 25 } };

        int V = 7;

        // length of the array
        int N = arr.length;

        System.out.println(countIntervals(arr, V, N));
    }
}

Python3

# Python3 program to count the number of
# intervals in which a given value lies
MAX_VAL = 200000

# Function to count the number of
# intervals in which a given value lies
def countIntervals(arr, V, N):

    # Variables to store overall minimumimum
    # and maximumimum of the intervals
    minimum = float("inf")
    maximum = 0

    # Frequency array to keep track of
    # how many of the given intervals
    # an element lies in
    freq = [0] * (MAX_VAL)

    for i in range(0, N):
        li = arr[i][0]
        freq[li] = freq[li] + 1
        ri = arr[i][1]
        freq[ri + 1] = freq[ri + 1] - 1

        if li < minimum:
            minimum = li

        if ri > maximum:
            maximum = ri

    # Constructing the frequency array
    for i in range(minimum, maximum + 1):
        freq[i] = freq[i] + freq[i - 1]

    return freq[V]

# Driver Code
if __name__ == "__main__":

    arr = [[1, 10], [5, 10], [15, 25],
           [7, 12], [20, 25]]

    V = 7

    # length of the array
    N = len(arr)

    print(countIntervals(arr, V, N))

# This code is contributed
# by Rituraj Jain

C#

// C# program to count the
// number of intervals in which
// a given value lies
using System;

class GFG {

    static  int MAX_VAL = 200000;

    // Function to count the
    // number of intervals in which
    // a given value lies
    static int countIntervals(int[,] arr, int V, int N)
    {
        // Variables to store overall minimum and
        // maximum of the intervals
        int min = int.MaxValue, max = int.MinValue;

        // Variables to store start and end of an interval
        int li, ri;

        // Frequency array to keep track of
        // how many of the given intervals an element lies in
        int[] freq = new int[MAX_VAL];

        for (int i = 0; i < N; i++) {
            li = arr[i,0];
            freq[li] = freq[li] + 1;
            ri = arr[i,1];
            freq[ri + 1] = freq[ri + 1] - 1;

            if (li < min)
                min = li;
            if (ri > max)
                max = ri;
        }

        // Constructing the frequency array
        for (int i = min; i <= max; i++)
            freq[i] = freq[i] + freq[i - 1];

        return freq[V];
    }

    // Driver code
    public static void Main()
    {
        int[,] arr = new int[,]{ { 1, 10 }, { 5, 10 },
        { 15, 25 }, { 7, 12 }, { 20, 25 } };

        int V = 7;

        // length of the array
        int N = arr.Length/arr.Rank;

        Console.WriteLine(countIntervals(arr, V, N));
    }
}
// this code is contributed by mits

PHP

<?php
// PHP program to count the number of
// intervals in which a given value lies

$MAX_VAL = 200000;

// Function to count the number of
// intervals in which a given value lies
function countIntervals($arr, $V, $N)
{
    global $MAX_VAL;

    // Variables to store overall minimum
    // and maximum of the intervals
    $min = PHP_INT_MAX;
    $max = 0;

    // Variables to store start and
    // end of an interval
    $li = 0;
    $ri = 0;

    // Frequency array to keep track of
    // how many of the given intervals
    // an element lies in
    $freq = array_fill(0, $MAX_VAL, 0);

    for ($i = 0; $i < $N; $i++)
    {
        $li = $arr[$i][0];
        $freq[$li] = $freq[$li] + 1;
        $ri = $arr[$i][1];
        $freq[$ri + 1] = $freq[$ri + 1] - 1;

        if ($li < $min)
            $min = $li;
        if ($ri > $max)
            $max = $ri;
    }

    // Constructing the frequency array
    for ($i = $min; $i <= $max; $i++)
        $freq[$i] = $freq[$i] + $freq[$i - 1];

    return $freq[$V];
}

// Driver code
$arr = array(array( 1, 10 ),
             array( 5, 10 ),
             array( 15, 25 ),
             array( 7, 12 ),
             array( 20, 25 ));

$V = 7;

// length of the array
$N = count($arr);

echo (countIntervals($arr, $V, $N));

// This code is contributed by mits
?>

Javascript

<script>
    // Javascript program to count the
    // number of intervals in which
    // a given value lies

    let MAX_VAL = 200000;

    // Function to count the
    // number of intervals in which
    // a given value lies
    function countIntervals(arr, V, N)
    {
        // Variables to store overall minimum and
        // maximum of the intervals
        let min = Number.MAX_VALUE, max = Number.MIN_VALUE;

        // Variables to store start and end of an interval
        let li, ri;

        // Frequency array to keep track of
        // how many of the given intervals an element lies in
        let freq = new Array(MAX_VAL);
        freq.fill(0);

        for (let i = 0; i < N; i++) {
            li = arr[i][0];
            freq[li] = freq[li] + 1;
            ri = arr[i][1];
            freq[ri + 1] = freq[ri + 1] - 1;

            if (li < min)
                min = li;
            if (ri > max)
                max = ri;
        }

        // Constructing the frequency array
        for (let i = min; i <= max; i++)
            freq[i] = freq[i] + freq[i - 1];

        return freq[V];
    }

    let arr = [ [ 1, 10 ], [ 5, 10 ],
                [ 15, 25 ], [ 7, 12 ], [ 20, 25 ] ];

    let V = 7;

    // length of the array
    let N = arr.length;

    document.write(countIntervals(arr, V, N));

// This code is contributed by divyeshrabadiya07.
</script>

Output:

3

Time Complexity: O(n)

Auxiliary Space: O(MAX)