Count Subarrays with Consecutive elements differing by 1
Last Updated :
16 Mar, 2023
Given an array arr[] of N integers. The task is to count the total number of subarrays of the given array such that the difference between the consecutive elements in the subarrays is one. That is, for any index 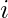 in the subarrays, arr[i+1] – arr[i] = 1.
in the subarrays, arr[i+1] – arr[i] = 1.
Note: Do not consider subarrays with a single element.
Examples:
Input : arr[] = {1, 2, 3}
Output : 3
The subarrays are {1, 2}. {2, 3} and {1, 2, 3}
Input : arr[] = {1, 2, 3, 5, 6, 7}
Output : 6
Naive Approach: A simple approach is to run two nested loops and check every subarray and calculate the count of subarrays with consecutive elements differing by 1.
C++
#include <iostream>
using namespace std;
int countSubarrays(int arr[], int n) {
int count = 0;
for (int i = 0; i < n; i++) {
int j = i + 1;
while (j < n && arr[j] - arr[j-1] == 1) {
j++;
}
count += (j - i) * (j - i - 1) / 2;
i = j - 1;
}
return count;
}
int main() {
int arr[] = {1, 2, 3};
int n = sizeof(arr)/sizeof(arr[0]);
int count = countSubarrays(arr, n);
cout << "Total number of subarrays with consecutive elements differing by 1: " << count << endl;
return 0;
}
|
Java
import java.util.*;
public class Main {
public static int countSubarrays(int[] arr, int n) {
int count = 0;
for (int i = 0; i < n; i++) {
int j = i + 1;
while (j < n && arr[j] - arr[j-1] == 1) {
j++;
}
count += (j - i) * (j - i - 1) / 2;
i = j - 1;
}
return count;
}
public static void main(String[] args) {
int[] arr = {1, 2, 3};
int n = arr.length;
int count = countSubarrays(arr, n);
System.out.println("Total number of subarrays with consecutive elements differing by 1: " + count);
}
}
|
Python3
def countSubarrays(arr, n):
count = 0
i = 0
while i < n:
j = i + 1
while j < n and arr[j] - arr[j-1] == 1:
j += 1
count += (j - i) * (j - i - 1) // 2
i = j
return count
arr = [1, 2, 3]
n = len(arr)
count = countSubarrays(arr, n)
print("Total number of subarrays with consecutive elements differing by 1:", count)
|
C#
using System;
class Gfg
{
static int countSubarrays(int[] arr, int n)
{
int count = 0;
for (int i = 0; i < n; i++) {
int j = i + 1;
while (j < n && arr[j] - arr[j-1] == 1) {
j++;
}
count += (j - i) * (j - i - 1) / 2;
i = j - 1;
}
return count;
}
public static void Main()
{
int[] arr = {1, 2, 3};
int n = arr.Length;
int count = countSubarrays(arr, n);
Console.WriteLine("Total number of subarrays with consecutive elements differing by 1: " + count);
}
}
|
Javascript
function countSubarrays(arr, n) {
let count = 0;
for (let i = 0; i < n; i++) {
let j = i + 1;
while (j < n && arr[j] - arr[j - 1] === 1) {
j++;
}
count += ((j - i) * (j - i - 1)) / 2;
i = j - 1;
}
return count;
}
const arr = [1, 2, 3];
const n = arr.length;
const count = countSubarrays(arr, n);
console.log(
`Total number of subarrays with consecutive elements differing by 1: ${count}`
);
|
OutputTotal number of subarrays with consecutive elements differing by 1: 3
Time Complexity: O(N²)
Auxiliary Space: O(1)
Efficient Approach: An efficient approach is to observe that in an array of length say K, the total number of subarrays of size greater than 1 = (K)*(K-1)/2.
So, the idea is to traverse the array by using two pointers to calculate subarrays with consecutive elements in a window of maximum length and then calculate all subarrays in that window using the above formula.
Below is the step-by-step algorithm:
- Take two pointers to say fast and slow, for maintaining a window of consecutive elements.
- Start traversing the array.
- If elements differ by 1 increment only the fast pointer.
- Else, calculate the length of the current window between the indexes fast and slow.
Below is the implementation of the given approach:
C++
#include <iostream>
using namespace std;
int subarrayCount(int arr[], int n)
{
int result = 0;
int fast = 0, slow = 0;
for (int i = 1; i < n; i++) {
if (arr[i] - arr[i - 1] == 1) {
fast++;
}
else {
int len = fast - slow + 1;
result += len * (len - 1) / 2;
fast = i;
slow = i;
}
}
if (fast != slow) {
int len = fast - slow + 1;
result += len * (len - 1) / 2;
}
return result;
}
int main()
{
int arr[] = { 1, 2, 3, 5, 6, 7 };
int n = sizeof(arr) / sizeof(arr[0]);
cout << subarrayCount(arr, n);
return 0;
}
|
Java
class cfg
{
static int subarrayCount(int arr[], int n)
{
int result = 0;
int fast = 0, slow = 0;
for (int i = 1; i < n; i++) {
if (arr[i] - arr[i - 1] == 1) {
fast++;
}
else {
int len = fast - slow + 1;
result += len * (len - 1) / 2;
fast = i;
slow = i;
}
}
if (fast != slow) {
int len = fast - slow + 1;
result += len * (len - 1) / 2;
}
return result;
}
public static void main(String[] args)
{
int arr[] = { 1, 2, 3, 5, 6, 7 };
int n = arr.length;
System.out.println(subarrayCount(arr, n));
}
}
|
Python3
def subarrayCount(arr, n) :
result = 0
fast, slow = 0, 0
for i in range(1, n) :
if (arr[i] - arr[i - 1] == 1) :
fast += 1
else :
length = fast - slow + 1
result += length * (length - 1) // 2;
fast = i
slow = i
if (fast != slow) :
length = fast - slow + 1
result += length * (length - 1) // 2;
return result
if __name__ == "__main__" :
arr = [ 1, 2, 3, 5, 6, 7 ]
n = len(arr)
print(subarrayCount(arr, n))
|
C#
using System;
class cfg
{
static int subarrayCount(int []arr, int n)
{
int result = 0;
int fast = 0, slow = 0;
for (int i = 1; i < n; i++) {
if (arr[i] - arr[i - 1] == 1) {
fast++;
}
else {
int len = fast - slow + 1;
result += len * (len - 1) / 2;
fast = i;
slow = i;
}
}
if (fast != slow) {
int len = fast - slow + 1;
result += len * (len - 1) / 2;
}
return result;
}
public static void Main()
{
int []arr = { 1, 2, 3, 5, 6, 7 };
int n = arr.Length;
Console.WriteLine(subarrayCount(arr, n));
}
}
|
PHP
<?php
function subarrayCount($arr, $n)
{
$result = 0;
$fast = 0; $slow = 0;
for ($i = 1; $i < $n; $i++)
{
if ($arr[$i] - $arr[$i - 1] == 1)
{
$fast++;
}
else
{
$len = $fast - $slow + 1;
$result += $len * ($len - 1) / 2;
$fast = $i;
$slow = $i;
}
}
if ($fast != $slow)
{
$len = $fast - $slow + 1;
$result += $len * ($len - 1) / 2;
}
return $result;
}
$arr = array(1, 2, 3, 5, 6, 7);
$n = sizeof($arr);
echo subarrayCount($arr, $n);
?>
|
Javascript
<script>
function subarrayCount(arr , n) {
var result = 0;
var fast = 0, slow = 0;
for (i = 1; i < n; i++) {
if (arr[i] - arr[i - 1] == 1) {
fast++;
} else {
var len = fast - slow + 1;
result += len * (len - 1) / 2;
fast = i;
slow = i;
}
}
if (fast != slow) {
var len = fast - slow + 1;
result += len * (len - 1) / 2;
}
return result;
}
var arr = [ 1, 2, 3, 5, 6, 7 ];
var n = arr.length;
document.write(subarrayCount(arr, n));
</script>
|
Complexity Analysis:
- Time Complexity: O(N), as we are using a loop to traverse N times so the complexity for the program will be O(N).
- Auxiliary Space: O(1), as we are not using any extra space.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...