Count of strings where adjacent characters are of difference one

Given a number n, count the number of strings of length n such that every string has adjacent characters with a difference between ASCII values as 1.

Examples: 

Input :  N = 1
Output : Total strings are 26
         Explanation : For N=1, strings 
         are a, b, c,, ...., x, y, z 

Input :  N = 2
Output : Total strings are 50
         Explanation : For N = 2, strings
         are ab, ba, bc, cb, .., yx, yz, zy

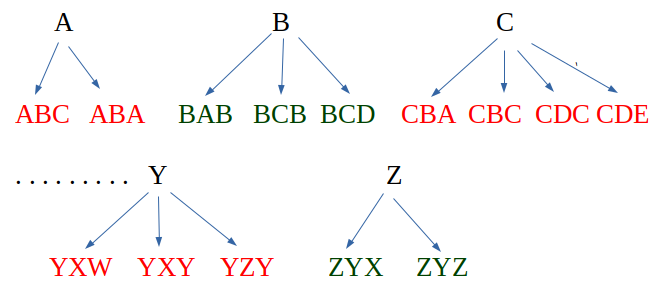
For strings starting with character ‘A’ and length ‘i’, we consider all strings of length ‘i-1’ and starting with character ‘B’
For strings starting with character ‘G’ and length ‘i’, we consider all strings of length ‘i-1’ and starting with character ‘H’ and all strings of length ‘i-1’ and starting with ‘F’.
We take the base case for n = 1, and set result for all 26 characters as 1. This simply means when 1 character string is consider all alphabets from a-z are taken only once.
For N = 2, 

For N = 3, 

Conclusion : For N = n

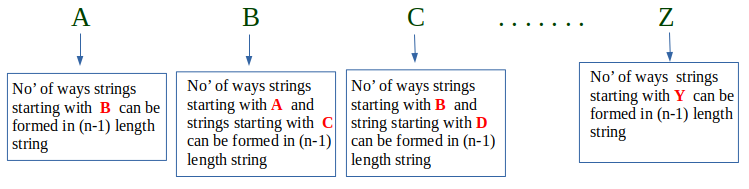
countAdjacent(n)
    dp[i][j] finally stores count of strings
             of length i and starting with 
             character j.

    Initialize dp[n+1][27] as 0
    Initialize dp[1][j] = 1 where j = 0 to 25
    for i = 2 to n
      for j = 0 to 25
         if (j = 0)
           dp[i][j] = dp[i-1][j+1];
         else
           dp[i][j] = dp[i-1][j-1] + dp[i-1][j+1];
    Sum of n-th row from 0 to 25 is the result.

Implementation:

C++

// CPP Program to count strings with adjacent
// characters.
#include <bits/stdc++.h>
using namespace std;

int countStrs(int n)
{
    long int dp[n + 1][27];

    // Initializing arr[n+1][27] to 0
    memset(dp, 0, sizeof(dp));

    // Initializing 1st row all 1 from 0 to 25
    for (int i = 0; i <= 25; i++)
        dp[1][i] = 1;

    // Begin evaluating from i=2 since 1st row is set
    for (int i = 2; i <= n; i++) {
        for (int j = 0; j <= 25; j++)

            // j=0 is 'A' which can make strings
            // of length i using strings of length
            // i-1 and starting with 'B'
            if (j == 0)
                dp[i][j] = dp[i - 1][j + 1];
            else
                dp[i][j] = (dp[i - 1][j - 1] +
                            dp[i - 1][j + 1]);
    }

    // Our result is sum of last row.
    long int sum = 0;
    for (int i = 0; i <= 25; i++)
        sum = (sum + dp[n][i]);
    return sum;
}

// Driver's Code
int main()
{
    int n = 3;
    cout << "Total strings are : " << countStrs(n);
    return 0;
}

Java

// Java Program to count strings
// with adjacent characters.
import java.io.*;
class GFG {

    static long countStrs(int n)
    {
        long[][] dp = new long[n + 1][27];

        // Initializing arr[n+1][27] to 0
        for (int i = 0; i < n + 1; i++) {
            for (int j = 0; j < 27; j++) {
                dp[i][j] = 0;
            }
        }

        // Initializing 1st row all 1 from 0 to 25
        for (int i = 0; i <= 25; i++) {
            dp[1][i] = 1;
        }

        // Begin evaluating from i=2
        // since 1st row is set
        for (int i = 2; i <= n; i++) {

            // j=0 is 'A' which can make strings
            for (int j = 0; j <= 25; j++)

            // of length i using strings of length
            // i-1 and starting with 'B'
            {
                if (j == 0) {
                    dp[i][j] = dp[i - 1][j + 1];
                }
                else {
                    dp[i][j] = (dp[i - 1][j - 1]
                                + dp[i - 1][j + 1]);
                }
            }
        }

        // Our result is sum of last row.
        long sum = 0;
        for (int i = 0; i <= 25; i++) {
            sum = (sum + dp[n][i]);
        }
        return sum;
    }

    // Driver Code
    public static void main(String[] args)
    {
        int n = 3;
        System.out.println("Total strings are : "
                           + countStrs(n));
    }
}

// This code is contributed by 29AjayKumar

Python 3

# Python3 Program to count strings with
# adjacent characters.
def countStrs(n):

    # Initializing arr[n+1][27] to 0
    dp = [[0 for j in range(27)]
             for i in range(n + 1)]

    # Initializing 1st row all 1 from 0 to 25
    for i in range(0, 26):
        dp[1][i] = 1

    # Begin evaluating from i=2 since
    # 1st row is set
    for i in range(2, n + 1):
        for j in range(0, 26):

            # j=0 is 'A' which can make strings
            # of length i using strings of length
            # i-1 and starting with 'B'
            if(j == 0):
                dp[i][j] = dp[i - 1][j + 1];
            else:
                dp[i][j] = (dp[i - 1][j - 1] +
                            dp[i - 1][j + 1])

    # Our result is sum of last row.
    sum = 0
    for i in range(0, 26):
        sum = sum + dp[n][i]

    return sum

# Driver's Code
if __name__ == "__main__":
    n = 3
    print("Total strings are : ", countStrs(n))

# This code is contributed by Sairahul Jella

C#

// C# Program to count strings with
// adjacent characters.
using System;

class GFG
{
    static long countStrs(int n)
    {
        long[,] dp = new long[n + 1, 27];

        // Initializing arr[n+1][27] to 0
        for(int i = 0; i < n + 1; i++)
            for(int j = 0; j < 27; j++)
                dp[i, j] = 0;

        // Initializing 1st row all 1 from 0 to 25
        for (int i = 0; i <= 25; i++)
            dp[1, i] = 1;

        // Begin evaluating from i=2 since 1st row is set
        for (int i = 2; i <= n; i++)
        {
            for (int j = 0; j <= 25; j++)

                // j=0 is 'A' which can make strings
                // of length i using strings of length
                // i-1 and starting with 'B'
                if (j == 0)
                    dp[i, j] = dp[i - 1, j + 1];
                else
                    dp[i, j] = (dp[i - 1, j - 1] +
                                dp[i - 1, j + 1]);
        }

        // Our result is sum of last row.
        long sum = 0;
        for (int i = 0; i <= 25; i++)
            sum = (sum + dp[n, i]);
        return sum;
    }

    // Driver Code
    static void Main()
    {
        int n = 3;
        Console.Write("Total strings are : " + countStrs(n));
    }
}

// This code is contributed by DrRoot_

Javascript

<script>
// JavaScript Program to count strings
// with adjacent characters.

    function countStrs(n)
    {
        let dp = new Array(n + 1);
        // Loop to create 2D array using 1D array
        for (var i = 0; i < dp.length; i++) {
            dp[i] = new Array(2);
        }

        // Initializing arr[n+1][27] to 0
        for (let i = 0; i < n + 1; i++)
        {
            for (let j = 0; j < 27; j++)
            {
                dp[i][j] = 0;
            }
        }

        // Initializing 1st row all 1 from 0 to 25
        for (let i = 0; i <= 25; i++)
        {
            dp[1][i] = 1;
        }

        // Begin evaluating from i=2
        // since 1st row is set
        for (let i = 2; i <= n; i++)
        {

            // j=0 is 'A' which can make strings
            for (let j = 0; j <= 25; j++)

            // of length i using strings of length
            // i-1 and starting with 'B'
            {
                if (j == 0)
                {
                    dp[i][j] = dp[i - 1][j + 1];
                }
                else
                {
                    dp[i][j] = (dp[i - 1][j - 1]
                            + dp[i - 1][j + 1]);
                }
            }
        }

        // Our result is sum of last row.
        let sum = 0;
        for (let i = 0; i <= 25; i++)
        {
            sum = (sum + dp[n][i]);
        }
        return sum;
    }

// Driver Code

    let n = 3;
    document.write("Total strings are : " +
                                        countStrs(n));

</script>

Output

Total strings are : 98

Time Complexity: O(26*n)
Auxiliary Space: O(26*n)

This article is contributed by Shubham Rana. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.