Count squares of size K inscribed in a square of size N

Given two integers N and K, the task is to find the number of squares of size K that is inscribed in a square of size N.

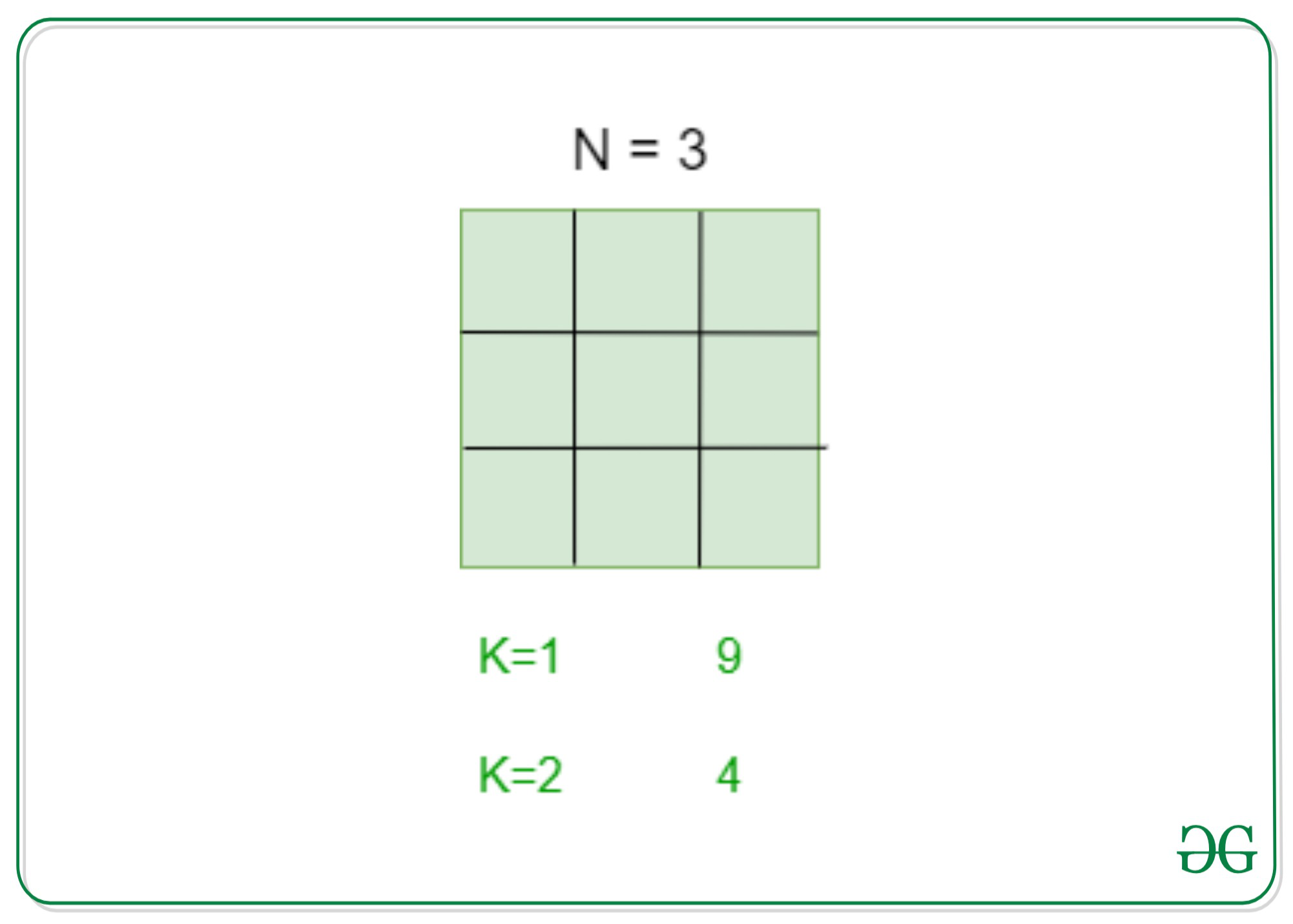
Examples:

Input: N = 4, K = 2
Output: 9
Explanation:
There are 9 squares of size 2 inscribed in a square of size 4.

Input: N = 5, K = 3
Output: 9
Explanation:
There are 9 squares of size 3 inscribed in a square of size 5.

Approach: The key observation to solve the problem is that the total number of squares in a square of size N is (N * (N + 1)* (2*N + 1)) / 6. Therefore, the total number of squares of size K possible from a square of size N are:

Below is the implementation of the above approach:

C++

// C++ implementation of the
// above approach

#include <iostream>
using namespace std;

// Function to calculate the number
// of squares of size K in a square
// of size N
int No_of_squares(int N, int K)
{
    // Stores the number of squares
    int no_of_squares = 0;

    no_of_squares
        = (N - K + 1) * (N - K + 1);

    return no_of_squares;
}

// Driver Code
int main()
{
    // Size of the
    // bigger square
    int N = 5;

    // Size of
    // smaller square
    int K = 3;
    cout << No_of_squares(N, K);
    return 0;
}

Java

// Java implementation of the
// above approach
import java.util.*;
class GFG{

// Function to calculate the
// number of squares of size
// K in a square of size N
static int No_of_squares(int N,
                         int K)
{
  // Stores the number
  // of squares
  int no_of_squares = 0;

  no_of_squares = (N - K + 1) *
                  (N - K + 1);

  return no_of_squares;
}

// Driver Code
public static void main(String[] args)
{
  // Size of the
  // bigger square
  int N = 5;

  // Size of
  // smaller square
  int K = 3;
  System.out.print(No_of_squares(N, K));
}
}

// This code is contributed by Princi Singh

Python3

# Python3 implementation of the
# above approach

# Function to calculate the
# number of squares of size
# K in a square of size N
def No_of_squares(N, K):

    # Stores the number
    # of squares
    no_of_squares = 0;
    no_of_squares = (N - K + 1) * (N - K + 1);
    return no_of_squares;

# Driver Code
if __name__ == '__main__':

    # Size of the
    # bigger square
    N = 5;

    # Size of
    # smaller square
    K = 3;
    print(No_of_squares(N, K));

# This code is contributed by 29AjayKumar

C#

// C# implementation of the
// above approach
using System;

class GFG{

// Function to calculate the
// number of squares of size
// K in a square of size N
static int No_of_squares(int N, int K)
{

    // Stores the number
    // of squares
    int no_of_squares = 0;

    no_of_squares = (N - K + 1) *
                    (N - K + 1);

    return no_of_squares;
}

// Driver Code
public static void Main(String[] args)
{

    // Size of the
    // bigger square
    int N = 5;

    // Size of
    // smaller square
    int K = 3;

    Console.Write(No_of_squares(N, K));
}
}

// This code is contributed by Amit Katiyar

Javascript

<script>

// JavaScript program for
// the above approach

// Function to calculate the
// number of squares of size
// K in a square of size N
function No_of_squares(N, K)
{
  // Stores the number
  // of squares
  let no_of_squares = 0;

  no_of_squares = (N - K + 1) *
                  (N - K + 1);

  return no_of_squares;
}

// Driver code

    // Size of the
  // bigger square
  let N = 5;

  // Size of
  // smaller square
  let K = 3;
  document.write(No_of_squares(N, K));

  // This code is contributed by splevel62.
</script>

Output:

9

Time Complexity: O(1) 
Auxiliary Space: O(1)