Count sequences of given length having non-negative prefix sums that can be generated by given values
Last Updated :
24 Feb, 2022
Given two integers M and X, the task is to find the number of sequences of length M that can be generated comprising X and -X such that their respective counts are equal and the prefix sum up to each index of the resulting sequence is non-negative.
Examples:
Input: M = 4, X = 5
Output: 2
Explanation:
There are only 2 possible sequences that have all possible prefix sums non-negative:
- {+5, +5, -5, -5}
- {+5, -5, +5, -5}
Input: M = 6, X = 2
Output: 5
Explanation:
There are only 5 possible sequences that have all possible prefix sums non-negative:
- {+2, +2, +2, -2, -2, -2}
- {+2, +2, -2, -2, +2, -2}
- {+2, -2, +2, -2, +2, -2}
- {+2, +2, -2, +2, -2, -2}
- {+2, -2, +2, +2, -2, -2}
Naive Approach: The simplest approach is to generate all possible arrangements of size M with the given integers +X and -X and find the prefix sum of each arrangement formed and count those sequences whose prefix sum array has only non-negative elements. Print the count of such sequence after the above steps.
Time Complexity: O((M*(M!))/((M/2)!)2)
Auxiliary Space: O(M)
Efficient Approach: The idea is to observe the pattern that for any sequence formed the number of positive X that has occurred at each index is always greater than or equal to the number of negative X that occurred. This is similar to the pattern of Catalan Numbers. In this case, check that at any point the number of positive X that occurred is always greater than or equal to the number of negative X that occurred which is the pattern of Catalan numbers. So the task is to find the Nth Catalan number where N = M/2.

where, KN is Nth the Catalan Number and 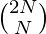 is the binomial coefficient.
is the binomial coefficient.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
unsigned long int binCoff(unsigned int n,
unsigned int r)
{
unsigned long int val = 1;
int i;
if (r > (n - r))
r = (n - r);
for (i = 0; i < r; i++) {
val *= (n - i);
val /= (i + 1);
}
return val;
}
void findWays(int M)
{
int n = M / 2;
unsigned long int a, b, ans;
a = binCoff(2 * n, n);
b = a / (n + 1);
cout << b;
}
int main()
{
int M = 4, X = 5;
findWays(M);
return 0;
}
|
Java
import java.io.*;
class GFG{
static long binCoff(long n, long r)
{
long val = 1;
int i;
if (r > (n - r))
r = (n - r);
for(i = 0; i < r; i++)
{
val *= (n - i);
val /= (i + 1);
}
return val;
}
static void findWays(int M)
{
int n = M / 2;
long a, b, ans;
a = binCoff(2 * n, n);
b = a / (n + 1);
System.out.print(b);
}
public static void main(String[] args)
{
int M = 4, X = 5;
findWays(M);
}
}
|
Python3
def binCoff(n, r):
val = 1
if (r > (n - r)):
r = (n - r)
for i in range(0, r):
val *= (n - i)
val //= (i + 1)
return val
def findWays(M):
n = M // 2
a = binCoff(2 * n, n)
b = a // (n + 1)
print(b)
if __name__ == '__main__':
M = 4
X = 5
findWays(M)
|
C#
using System;
class GFG{
static long binCoff(long n, long r)
{
long val = 1;
int i;
if (r > (n - r))
r = (n - r);
for(i = 0; i < r; i++)
{
val *= (n - i);
val /= (i + 1);
}
return val;
}
static void findWays(int M, int X)
{
int n = M / 2;
long a, b;
a = binCoff(2 * n, n);
b = a / (n + 1);
Console.WriteLine(b);
}
public static void Main()
{
int M = 4;
int X = 5;
findWays(M, X);
}
}
|
Javascript
<script>
function binCoff(n, r)
{
let val = 1;
let i;
if (r > (n - r))
r = (n - r);
for(i = 0; i < r; i++)
{
val *= (n - i);
val /= (i + 1);
}
return val;
}
function findWays(M)
{
let n = M / 2;
let a, b, ans;
a = binCoff(2 * n, n);
b = a / (n + 1);
document.write(b);
}
let M = 4, X = 5;
findWays(M);
</script>
|
Time Complexity: O(M)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...