Count possible decodings of a given Digit Sequence | Set 2
Last Updated :
05 Jan, 2022
Given an encoded string str consisting of digits and * which can be filled by any digit 1 – 9, the task is to find the number of ways to decode that string into a sequence of alphabets A-Z.
Note: The input string contains number from 0-9 and character ‘*’ only.
Examples:
Input: str = “1*”
Output: 18
Explanation:
Since * can be replaced by any value from (1-9),
The given string can be decoded as A[A-I] + [J-R] = 9 + 9 ways
Input: str = “12*3”
Output: 28
Naive Approach: A simple solution is to solve the problem using recursion considering all the possible decodings of the string.
Below is the recursion tree for the problem:
12*3
/ \
12*(3) 12(*3)
/ \ / \
12(*)(3) 1(2*)(3) 1(2)(*3) ""
/ \ \ /
1(2)(*)(3) "" "" ""
/
""
Efficient Approach: The idea is to solve the problem using Dynamic Programming using the optimal substructure for considering all the cases of the current and the previous digits of the string and their number of ways to decode the string.
Definition of the DP State: In this problem the ![Rendered by QuickLaTeX.com dp[i]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-77fe8dc11b0da172e838df5053e55d1a_l3.png) denotes the number of ways to decode the string upto the
denotes the number of ways to decode the string upto the 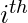 index.
index.
Initial DP States: Initially the value of the DP states are defined as below:
// Number of ways to decode
// an empty string
dp[0] = 1
// Number of ways to decode the
// first character
if (s[0] == '*')
dp[1] = 9 // 9 ways
else
dp[1] = 1
Optimal Sub-structure: There are generally two ways to decode the current character of the string:
- Including the current character as single-digit to decode: If the current character is used as single-digit then there can be generally two cases for the character to be:
- Case 1: If current character is equal to the
 , Then there are 9 possible ways to take any digit from [1-9] and decode it as any character from [A-Z].
, Then there are 9 possible ways to take any digit from [1-9] and decode it as any character from [A-Z].
if (current == "*")
dp[i] += 9 * dp[i-1]- Case 2: If current character is equal to any other digit from [0-9], Then the number of possible ways to decode is equal to the number of way to decode the string upto
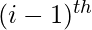 index.
index.
if (current != "*")
dp[i] += dp[i-1]- Including the current character as two-digits to decode: If the current character is to be decoded as two-digits then there are two possible cases:
- Case 1: If the previous character is equal to the
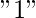 or
or 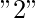 , then there can be two more possible subcases which will depend upon the current character:
, then there can be two more possible subcases which will depend upon the current character:
- Case 1.1: If the current character is equal to the
 , then total possible ways to decode are 9 if the previous character is 1, otherwise 6 if previous character is 2.
, then total possible ways to decode are 9 if the previous character is 1, otherwise 6 if previous character is 2. - Case 1.2: If the current character is less than equal to 6, Then the total number of possible way to decode the string will depend only on the number of way to decode upto the previous character. That is
![Rendered by QuickLaTeX.com dp[i-2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1072191aab574b3d1552e1b2abe0be42_l3.png)
- Case 2: If the previous character is
 , then there can be two more possible subcases which will depend upon the current character:
, then there can be two more possible subcases which will depend upon the current character:
- Case 2.1: If the current character is also
 , Then the total number of cases will be
, Then the total number of cases will be ![Rendered by QuickLaTeX.com 15 * dp[i-2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-39ffa567ceabd39bdc2225be417a9679_l3.png) , because the single digits of decoding ways of previous character must be already included.
, because the single digits of decoding ways of previous character must be already included. - Case 2.2: If the current character is less than 6, Then the total number of ways will be
![Rendered by QuickLaTeX.com 2*dp[i-2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d9a9cac31528689a896a580444e406b6_l3.png) , because then the number of ways to choose the digits of the first character is 2. That is [1, 2].
, because then the number of ways to choose the digits of the first character is 2. That is [1, 2]. - Case 2.3: If the current character is any digits, Then the total number of ways will be the number of ways to decode uptill the previous digit only. That is
![Rendered by QuickLaTeX.com dp[i-2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a21eeab3680f17dcca68a13da9231fdb_l3.png) .
.
C++
#include <bits/stdc++.h>
using namespace std;
int waysToDecode2(string s) {
int n = s.size();
vector<int> dp(n+1,0);
dp[0]=1;
if(s[0]=='0')
return 0;
dp[1]= ((s[0]=='*')? 9 : 1);
for(int i=2;i<=n;i++)
{
char first= s[i-2];
char second= s[i-1];
if(second=='*')
{
dp[i]+= 9*dp[i-1];
}
else if(second>'0')
dp[i]+=dp[i-1];
if(first=='1'|| first=='2')
{
if(second=='*')
{
if(first=='1')
dp[i]+= 9 * dp[i-2];
else if(first=='2')
dp[i]+= 6 * dp[i-2];
}
else if(((first-'0')* 10 +
(second-'0'))<= 26)
dp[i]+=dp[i-2];
}
else if(first=='*')
{
if(second=='*')
{
dp[i]+= 15 * dp[i-2];
}
else if(second<='6')
dp[i]+= 2* dp[i-2];
else
dp [i]+= dp[i-2];
}
}
return dp[n];
}
int main() {
string str = "12*3";
cout << waysToDecode2(str) << endl;
return 0;
}
|
Java
class GFG{
static int waysToDecode2(char []s)
{
int n = s.length;
int []dp = new int[n + 1];
dp[0] = 1;
if(s[0] == '0')
return 0;
dp[1] = ((s[0] == '*') ? 9 : 1);
for(int i = 2; i <= n; i++)
{
char first = s[i - 2];
char second = s[i - 1];
if(second == '*')
{
dp[i] += 9 * dp[i - 1];
}
else if(second > '0')
dp[i] += dp[i - 1];
if(first == '1' || first == '2')
{
if(second == '*')
{
if(first == '1')
dp[i] += 9 * dp[i - 2];
else if(first == '2')
dp[i] += 6 * dp[i - 2];
}
else if(((first - '0') * 10 +
(second - '0')) <= 26)
{
dp[i] += dp[i - 2];
}
}
else if(first == '*')
{
if(second == '*')
{
dp[i] += 15 * dp[i - 2];
}
else if(second <= '6')
{
dp[i] += 2 * dp[i - 2];
}
else
{
dp[i] += dp[i - 2];
}
}
}
return dp[n];
}
public static void main(String[] args)
{
String str = "12*3";
System.out.print(waysToDecode2(
str.toCharArray()) + "\n");
}
}
|
C#
using System;
class GFG{
static int waysToDecode2(char []s)
{
int n = s.Length;
int []dp = new int[n + 1];
dp[0] = 1;
if(s[0] == '0')
return 0;
dp[1] = ((s[0] == '*') ? 9 : 1);
for(int i = 2; i <= n; i++)
{
char first = s[i - 2];
char second = s[i - 1];
if(second == '*')
{
dp[i] += 9 * dp[i - 1];
}
else if(second > '0')
{
dp[i] += dp[i - 1];
}
if(first == '1' || first == '2')
{
if(second == '*')
{
if(first == '1')
{
dp[i] += 9 * dp[i - 2];
}
else if(first == '2')
{
dp[i] += 6 * dp[i - 2];
}
}
else if(((first - '0') * 10 +
(second - '0')) <= 26)
{
dp[i] += dp[i - 2];
}
}
else if(first == '*')
{
if(second == '*')
{
dp[i] += 15 * dp[i - 2];
}
else if(second <= '6')
{
dp[i] += 2 * dp[i - 2];
}
else
{
dp[i] += dp[i - 2];
}
}
}
return dp[n];
}
public static void Main(String[] args)
{
String str = "12*3";
Console.Write(waysToDecode2(
str.ToCharArray()) + "\n");
}
}
|
Javascript
<script>
function waysToDecode2(s)
{
let n = s.length;
let dp = Array.from({length: n+1}, (_, i) => 0);
dp[0] = 1;
if(s[0] == '0')
return 0;
dp[1] = ((s[0] == '*') ? 9 : 1);
for(let i = 2; i <= n; i++)
{
let first = s[i - 2];
let second = s[i - 1];
if(second == '*')
{
dp[i] += 9 * dp[i - 1];
}
else if(second > '0')
dp[i] += dp[i - 1];
if(first == '1' || first == '2')
{
if(second == '*')
{
if(first == '1')
dp[i] += 9 * dp[i - 2];
else if(first == '2')
dp[i] += 6 * dp[i - 2];
}
else if(((first - '0') * 10 +
(second - '0')) <= 26)
{
dp[i] += dp[i - 2];
}
}
else if(first == '*')
{
if(second == '*')
{
dp[i] += 15 * dp[i - 2];
}
else if(second <= '6')
{
dp[i] += 2 * dp[i - 2];
}
else
{
dp[i] += dp[i - 2];
}
}
}
return dp[n];
}
let str = "12*3";
document.write(waysToDecode2(
str.split('')) + "\n");
</script>
|
Python3
def waysToDecode2(s):
n = len(s)
dp = [0] * (n + 1)
dp[0] = 1
if s[0] == "0":
return 0
dp[1] = 9 if (s[0] == "*") else 1
for i in range(2, n+1):
first = s[i - 2]
second = s[i - 1]
if second == "*":
dp[i] += 9 * dp[i - 1]
elif second > "0":
dp[i] += dp[i - 1]
if first == "1" or first == "2":
if second == "*":
if first == "1":
dp[i] += 9 * dp[i - 2]
elif first == "2":
dp[i] += 6 * dp[i - 2]
elif (ord(first) - ord("0")) * 10 + (ord(second) - ord("0")) <= 26:
dp[i] += dp[i - 2]
elif first == "*":
if second == "*":
dp[i] += 15 * dp[i - 2]
elif second <= "6":
dp[i] += 2 * dp[i - 2]
else:
dp[i] += dp[i - 2]
return dp[n]
if __name__ == "__main__":
str = "12*3"
print(waysToDecode2(str))
|
Output:
28
- Time Complexity: O(N)
- Auxiliary Space: O(N)
Share your thoughts in the comments
Please Login to comment...