Count positive integers with 0 as a digit and maximum ‘d’ digits
Last Updated :
19 Sep, 2022
Given a number d, representing the number of digits of a number. Find the total count of positive integers which have at-least one zero in them and consist d or less digits.
Examples:
Input : d = 1
Output : 0
There's no natural number of 1 digit that contains a zero.
Input : d = 2
Output : 9
Input : d = 3
Output : 180
For d = 3, we've to count numbers from 1 to 999, that have
atleast one zero in them.
Similarly for d=4, we'd check every number from 1 to 9999.
This is mainly an extension of below post.
Count ‘d’ digit positive integers with 0 as a digit.
If we observe carefully the problem is very similar to the one which we had discussed in our first set. For a given d, we can get the required answer if we find numbers that have 0s and consist of digits 1, 2, 3….., d. Finally we can add them to get the output.
Below is the program for the same.
C++
#include<bits/stdc++.h>
using namespace std;
int findCount(int d)
{
return 9*(pow(10,d-1) - pow(9,d-1));
}
int findCountUpto(int d)
{
int totalCount = 0;
for (int i=1; i<=d; i++)
totalCount += findCount(i);
return totalCount;
}
int main()
{
int d = 1;
cout << findCountUpto(d) << endl;
d = 2;
cout << findCountUpto(d) << endl;
d = 4;
cout << findCountUpto(d) << endl;
return 0;
}
|
Java
import java.io.*;
import java.math.*;
class GFG {
static int findCount(int d)
{
return 9 * (int)((Math.pow(10, d - 1)
- Math.pow(9, d - 1)));
}
static int findCountUpto(int d)
{
int totalCount = 0;
for (int i = 1; i <= d; i++)
totalCount += findCount(i);
return totalCount;
}
public static void main(String args[])
{
int d = 1;
System.out.println(findCountUpto(d));
d = 2;
System.out.println( findCountUpto(d) );
d = 4;
System.out.println(findCountUpto(d));
}
}
|
Python3
import math
def findCountUpto(d) :
GP1_Sum = 9*((int)((math.pow(10,d))-1)//9)
GP2_Sum = 9*((int)((math.pow(9,d))-1)//8)
return GP1_Sum - GP2_Sum
d = 1
print(findCountUpto(d))
d = 2
print(findCountUpto(d))
d = 4
print(findCountUpto(d))
|
C#
using System;
class GFG {
static int findCount(int d)
{
return 9 * (int)((Math.Pow(10, d - 1)
- Math.Pow(9, d - 1)));
}
static int findCountUpto(int d)
{
int totalCount = 0;
for (int i = 1; i <= d; i++)
totalCount += findCount(i);
return totalCount;
}
public static void Main()
{
int d = 1;
Console.WriteLine(findCountUpto(d));
d = 2;
Console.WriteLine( findCountUpto(d) );
d = 4;
Console.WriteLine(findCountUpto(d));
}
}
|
PHP
<?php
function findCount($d)
{
return 9 * (pow(10, $d - 1) -
pow(9, $d - 1));
}
function findCountUpto($d)
{
$totalCount = 0;
for ($i = 1; $i <= $d; $i++)
$totalCount += findCount($i);
return $totalCount;
}
{
$d = 1;
echo findCountUpto($d),"\n" ;
$d = 2;
echo findCountUpto($d),"\n" ;
$d = 4;
echo findCountUpto($d) ;
return 0;
}
?>
|
Javascript
<script>
function findCount(d)
{
return 9 * ((Math.pow(10, d - 1)
- Math.pow(9, d - 1)));
}
function findCountUpto(d)
{
let totalCount = 0;
for (let i = 1; i <= d; i++)
totalCount += findCount(i);
return totalCount;
}
let d = 1;
document.write(findCountUpto(d) + "<br/>");
d = 2;
document.write( findCountUpto(d) + "<br/>" );
d = 4;
document.write(findCountUpto(d) + "<br/>");
</script>
|
Output :
0
9
2619
Time Complexity : O(d)
Auxiliary Space : O(1)
Can we make the solution more efficient ?
Yes, if we see closely, the required answer is obtained using the sum of following two Geometric Progressions:
i'th term of G.P. 1 = 9*10i - 1 where 1 <= i <= d
i'th term of G.P. 2 = 9*9i - 1 where 1 <= i <= d
The final answer is nothing but,
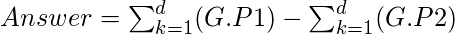 Sum of G.P 1 = 9*(10d - 1)/(10-1) = 9*(10d - 1)/9Similarly,Sum of G.P 2 = 9*(9d - 1)/(9-1) = 9*(9d - 1)/8Using the above facts, we can optimize the solution to run in O(1)
Sum of G.P 1 = 9*(10d - 1)/(10-1) = 9*(10d - 1)/9Similarly,Sum of G.P 2 = 9*(9d - 1)/(9-1) = 9*(9d - 1)/8Using the above facts, we can optimize the solution to run in O(1)
Below is an efficient program for the same.
C++
#include<bits/stdc++.h>
using namespace std;
int findCountUpto(int d)
{
int GP1_Sum = 9*((pow(10,d)-1)/9);
int GP2_Sum = 9*((pow(9,d)-1)/8);
return GP1_Sum - GP2_Sum;
}
int main()
{
int d = 1;
cout << findCountUpto(d) << endl;
d = 2;
cout << findCountUpto(d) << endl;
d = 4;
cout << findCountUpto(d) << endl;
return 0;
}
|
Java
import java.io.*;
import java.math.*;
class GFG {
static int findCountUpto(int d)
{
int GP1_Sum = 9 * ((int)((Math.pow(10, d)) - 1) / 9);
int GP2_Sum = 9 * ((int)((Math.pow(9, d)) - 1) / 8);
return GP1_Sum - GP2_Sum;
}
public static void main(String args[])
{
int d = 1;
System.out.println(findCountUpto(d));
d = 2;
System.out.println(findCountUpto(d));
d = 4;
System.out.println(findCountUpto(d));
}
}
|
Python3
import math
def findCount(d) :
return 9*(pow(10,d-1) - pow(9,d-1));
def findCountUpto(d) :
totalCount = 0
for i in range(1,d+1) :
totalCount = totalCount + findCount(i)
return totalCount
d = 1
print(findCountUpto(d))
d = 2
print(findCountUpto(d))
d = 4
print(findCountUpto(d))
|
C#
using System;
class GFG {
static int findCountUpto(int d)
{
int GP1_Sum = 9 * ((int)((Math.Pow(10,
d)) - 1) / 9);
int GP2_Sum = 9 * ((int)((Math.Pow(9,
d)) - 1) / 8);
return GP1_Sum - GP2_Sum;
}
public static void Main()
{
int d = 1;
Console.WriteLine(findCountUpto(d));
d = 2;
Console.WriteLine(findCountUpto(d));
d = 4;
Console.WriteLine(findCountUpto(d));
}
}
|
PHP
<?php
function findCountUpto($d)
{
$GP1_Sum = 9 * ((pow(10, $d) - 1) / 9);
$GP2_Sum = 9 * ((pow(9, $d) - 1) / 8);
return $GP1_Sum - $GP2_Sum;
}
$d = 1;
echo findCountUpto($d),"\n";
$d = 2;
echo findCountUpto($d),"\n";
$d = 4;
echo findCountUpto($d) ,"\n";
?>
|
Javascript
function findCountUpto(d)
{
let GP1_Sum = 9 * ((Math.pow(10, d) - 1) / 9);
let GP2_Sum = 9 * ((Math.pow(9, d) - 1) / 8);
return GP1_Sum - GP2_Sum;
}
let d = 1;
document.write(findCountUpto(d) + "<br>");
d = 2;
document.write(findCountUpto(d) + "<br>");
d = 4;
document.write(findCountUpto(d) + "<br>");
|
Output :
0
9
2619
Time Complexity : O(logd) because inbuilt pow function is used
Auxiliary Space : O(1)
In the next set we’d see another problem of increased difficulty that can be solved using very similar technique.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...