Count pairs with Bitwise-AND as even number
Last Updated :
18 Apr, 2023
Given an array of 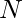 integers. The task is to find the number of pairs (i, j) such that A[i] & A[j] is even.
integers. The task is to find the number of pairs (i, j) such that A[i] & A[j] is even.
Examples:
Input: N = 4, A[] = { 5, 1, 3, 2 }
Output: 3
Since pair of A[] are:
( 5, 1 ), ( 5, 3 ), ( 5, 2 ), ( 1, 3 ), ( 1, 2 ), ( 3, 2 )
5 AND 1 = 1, 5 AND 3 = 1, 5 AND 2 = 0,
1 AND 3 = 1, 1 AND 2 = 0,
3 AND 2 = 2
Total even pair A( i, j ) = 3
Input : N = 6, A[] = { 5, 9, 0, 6, 7, 3 }
Output : 9
Since pair of A[] =
( 5, 9 ) = 1, ( 5, 0 ) = 0, ( 5, 6 ) = 4, ( 5, 7 ) = 5, ( 5, 3 ) = 1,
( 9, 0 ) = 0, ( 9, 6 ) = 0, ( 9, 7 ) = 1, ( 9, 3 ) = 1,
( 0, 6 ) = 0, ( 0, 7 ) = 0, ( 0, 3 ) = 0,
( 6, 7 ) = 6, ( 6, 3 ) = 2,
( 7, 3 ) = 3
A Naive Approach is to check for every pair and print the count of pairs which are even.
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
int findevenPair(int A[], int N)
{
int i, j;
int evenPair = 0;
for (i = 0; i < N; i++) {
for (j = i + 1; j < N; j++) {
if ((A[i] & A[j]) % 2 == 0)
evenPair++;
}
}
return evenPair;
}
int main()
{
int a[] = { 5, 1, 3, 2 };
int n = sizeof(a) / sizeof(a[0]);
cout << findevenPair(a, n) << endl;
return 0;
}
|
C
#include <stdio.h>
int findevenPair(int A[], int N)
{
int i, j;
int evenPair = 0;
for (i = 0; i < N; i++) {
for (j = i + 1; j < N; j++) {
if ((A[i] & A[j]) % 2 == 0)
evenPair++;
}
}
return evenPair;
}
int main()
{
int a[] = { 5, 1, 3, 2 };
int n = sizeof(a) / sizeof(a[0]);
printf("%d\n",findevenPair(a, n));
return 0;
}
|
Java
import java.io.*;
class GFG
{
static int findevenPair(int []A,
int N)
{
int i, j;
int evenPair = 0;
for (i = 0; i < N; i++)
{
for (j = i + 1; j < N; j++)
{
if ((A[i] & A[j]) % 2 == 0)
evenPair++;
}
}
return evenPair;
}
public static void main (String[] args)
{
int []a = { 5, 1, 3, 2 };
int n = a.length;
System.out.println(findevenPair(a, n));
}
}
|
Python3
def findevenPair(A, N):
evenPair = 0
for i in range(0, N):
for j in range(i + 1, N):
if ((A[i] & A[j]) % 2 == 0):
evenPair += 1
return evenPair
a = [ 5, 1, 3, 2 ]
n = len(a)
print(findevenPair(a, n))
|
C#
using System;
class GFG
{
static int findevenPair(int []A,
int N)
{
int i, j;
int evenPair = 0;
for (i = 0; i < N; i++)
{
for (j = i + 1; j < N; j++)
{
if ((A[i] & A[j]) % 2 == 0)
evenPair++;
}
}
return evenPair;
}
public static void Main ()
{
int []a = { 5, 1, 3, 2 };
int n = a.Length;
Console.WriteLine(findevenPair(a, n));
}
}
|
PHP
<?php
function findevenPair($A, $N)
{
$evenPair = 0;
for ($i = 0; $i < $N; $i++)
{
for ($j = $i + 1; $j < $N; $j++)
{
if (($A[$i] & $A[$j]) % 2 == 0)
$evenPair++;
}
}
return $evenPair;
}
$a = array(5, 1, 3, 2 );
$n = sizeof($a);
echo findevenPair($a, $n);
?>
|
Javascript
<script>
function findevenPair(A, N)
{
let i, j;
let evenPair = 0;
for (i = 0; i < N; i++) {
for (j = i + 1; j < N; j++) {
if ((A[i] & A[j]) % 2 == 0)
evenPair++;
}
}
return evenPair;
}
let a = [ 5, 1, 3, 2 ];
let n = a.length;
document.write(findevenPair(a, n));
</script>
|
Time Complexity: O(N2)
Auxiliary Space: O(1)
An Efficient Approach will be to observe that the bitwise AND of two numbers will be even if atleast one of the two numbers is even. So, count all the odd numbers in the array say count. Now, number of pairs with both odd elements will be count*(count-1)/2.
Therefore, number of elements with atleast one even element will be:
Total Pairs - Count of pair with both odd elements
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
int findevenPair(int A[], int N)
{
int count = 0;
for (int i = 0; i < N; i++)
if (A[i] % 2 != 0)
count++;
int oddCount = count * (count - 1) / 2;
return (N * (N - 1) / 2) - oddCount;
}
int main()
{
int a[] = { 5, 1, 3, 2 };
int n = sizeof(a) / sizeof(a[0]);
cout << findevenPair(a, n) << endl;
return 0;
}
|
C
#include <stdio.h>
int findevenPair(int A[], int N)
{
int count = 0;
for (int i = 0; i < N; i++)
if (A[i] % 2 != 0)
count++;
int oddCount = count * (count - 1) / 2;
return (N * (N - 1) / 2) - oddCount;
}
int main()
{
int a[] = { 5, 1, 3, 2 };
int n = sizeof(a) / sizeof(a[0]);
printf("%d\n",findevenPair(a, n));
return 0;
}
|
Java
import java.io.*;
class GFG {
static int findevenPair(int A[], int N)
{
int count = 0;
for (int i = 0; i < N; i++)
if (A[i] % 2 != 0)
count++;
int oddCount = count * (count - 1) / 2;
return (N * (N - 1) / 2) - oddCount;
}
public static void main (String[] args) {
int a[] = { 5, 1, 3, 2 };
int n =a.length;
System.out.print( findevenPair(a, n));
}
}
|
Python3
def findevenPair(A, N):
count = 0
for i in range(0, N):
if (A[i] % 2 != 0):
count += 1
oddCount = count * (count - 1) / 2
return (int)((N * (N - 1) / 2) - oddCount)
a = [5, 1, 3, 2 ]
n = len(a)
print(findevenPair(a, n))
|
C#
using System;
public class GFG{
static int findevenPair(int []A, int N)
{
int count = 0;
for (int i = 0; i < N; i++)
if (A[i] % 2 != 0)
count++;
int oddCount = count * (count - 1) / 2;
return (N * (N - 1) / 2) - oddCount;
}
static public void Main (){
int []a = { 5, 1, 3, 2 };
int n =a.Length;
Console.WriteLine( findevenPair(a, n));
}
}
|
PHP
<?php
function findevenPair($A, $N)
{
$count = 0;
for ($i = 0; $i < $N; $i++)
if ($A[$i] % 2 != 0)
$count++;
$oddCount = $count * ($count - 1) / 2;
return ($N * ($N - 1) / 2) - $oddCount;
}
$a = array(5, 1, 3, 2);
$n = sizeof($a);
echo findevenPair($a, $n) . "\n";
?>
|
Javascript
<script>
function findevenPair(A, N)
{
let count = 0;
for(let i = 0; i < N; i++)
if (A[i] % 2 != 0)
count++;
let oddCount = parseInt((count *
(count - 1)) / 2);
return parseInt((N * (N - 1)) / 2) - oddCount;
}
let a = [ 5, 1, 3, 2 ];
let n = a.length;
document.write(findevenPair(a, n));
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(1)
Another Method: we observe that bitwise AND of any two numbers will be even if any one of them will be even, no matter what is another number, if one number is even bitwise ANd of that number with any number will be even.
so if our array has an even number count as evenNumCount then the total no. of pair whose bitwise AND is even will be
(n-1)*evenNumCount - (evenNumCount*(evenNumCount-1))/2
here second term (evenNumCount*(evenNumCount-1))/2 will be subtracted from actual ans as we counted (even, even) pair twice.
C++
#include <iostream>
using namespace std;
int findevenPair(int A[], int N)
{
int evenNumCount = 0;
for (int i = 0; i < N; i++)
if (A[i] % 2 == 0)
evenNumCount++;
return (N - 1) * evenNumCount - ((evenNumCount * (evenNumCount - 1)) / 2);
}
int main()
{
int a[] = { 5, 1, 3, 2 };
int n = sizeof(a) / sizeof(a[0]);
cout << findevenPair(a, n) << endl;
return 0;
}
|
Java
import java.util.*;
public class Main {
static int findevenPair(int A[], int N)
{
int evenNumCount = 0;
for (int i = 0; i < N; i++)
if (A[i] % 2 == 0)
evenNumCount++;
return (N - 1) * evenNumCount
- ((evenNumCount * (evenNumCount - 1)) / 2);
}
public static void main(String[] args)
{
int a[] = { 5, 1, 3, 2 };
int n = a.length;
System.out.println(findevenPair(a, n));
}
}
|
C#
using System;
public class MainClass {
public static int FindevenPair(int[] A, int N)
{
int evenNumCount = 0;
for (int i = 0; i < N; i++)
if (A[i] % 2 == 0)
evenNumCount++;
return (N - 1) * evenNumCount
- ((evenNumCount * (evenNumCount - 1)) / 2);
}
public static void Main()
{
int[] a = { 5, 1, 3, 2 };
int n = a.Length;
Console.WriteLine(FindevenPair(a, n));
}
}
|
Javascript
function findevenPair(A, N) {
let evenNumCount = 0;
for (let i = 0; i < N; i++) {
if (A[i] % 2 === 0) {
evenNumCount++;
}
}
return (N - 1) * evenNumCount - ((evenNumCount * (evenNumCount - 1)) / 2);
}
const a = [5, 1, 3, 2];
const n = a.length;
console.log(findevenPair(a, n));
|
Python3
def findevenPair(A, N):
evenNumCount = 0
for i in range(N):
if A[i] % 2 == 0:
evenNumCount += 1
return (N - 1) * evenNumCount - ((evenNumCount * (evenNumCount - 1)) // 2)
a = [5, 1, 3, 2]
n = len(a)
print(findevenPair(a, n))
|
Time Complexity: O(N)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...