Count pairs of numbers from 1 to N with Product divisible by their Sum
Last Updated :
29 Jun, 2022
Given a number 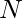 . The task is to count pairs (x, y) such that x*y is divisible by (x+y) and the condition 1 <= x < y < N holds true.
. The task is to count pairs (x, y) such that x*y is divisible by (x+y) and the condition 1 <= x < y < N holds true.
Examples:
Input : N = 6
Output : 1
Explanation: The only pair is (3, 6) which satisfies
all of the given condition, 3<6 and 18%9=0.
Input : N = 15
Output : 4
The basic approach is to iterate using two loops carefully maintaining the given condition 1 <= x < y < N and generate all possible valid pairs and count such pairs for which the product of their values is divisible by sum.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countPairs(int n)
{
int count = 0;
for (int x = 1; x < n; x++) {
for (int y = x + 1; y <= n; y++) {
if ((y * x) % (y + x) == 0)
count++;
}
}
return count;
}
int main()
{
int n = 15;
cout << countPairs(n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int countPairs(int n)
{
int count = 0;
for (int x = 1; x < n; x++) {
for (int y = x + 1; y <= n; y++) {
if ((y * x) % (y + x) == 0)
count++;
}
}
return count;
}
public static void main (String[] args) {
int n = 15;
System.out.println(countPairs(n));
}
}
|
Python3
def countPairs(n):
count = 0
for x in range(1, n):
for y in range(x + 1, n + 1):
if ((y * x) % (y + x) == 0):
count += 1
return count
n = 15
print(countPairs(n))
|
C#
using System;
class GFG
{
static int countPairs(int n)
{
int count = 0;
for (int x = 1; x < n; x++)
{
for (int y = x + 1; y <= n; y++)
{
if ((y * x) % (y + x) == 0)
count++;
}
}
return count;
}
public static void Main ()
{
int n = 15;
Console.WriteLine(countPairs(n));
}
}
|
PHP
<?php
function countPairs($n)
{
$count = 0;
for ($x = 1; $x < $n; $x++)
{
for ($y = $x + 1; $y <= $n; $y++)
{
if (($y * $x) % ($y + $x) == 0)
$count++;
}
}
return $count;
}
$n = 15;
echo countPairs($n);
?>
|
Javascript
<script>
function countPairs(n)
{
let count = 0;
for (let x = 1; x < n; x++) {
for (let y = x + 1; y <= n; y++) {
if ((y * x) % (y + x) == 0)
count++;
}
}
return count;
}
let n = 15;
document.write(countPairs(n));
</script>
|
Time Complexity : O(N2)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...