Count pairs of numbers from 1 to N with Product divisible by their Sum

Given a number 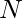. The task is to count pairs (x, y) such that x*y is divisible by (x+y) and the condition 1 <= x < y < N holds true.
Examples: 

Input : N = 6
Output : 1
Explanation: The only pair is (3, 6) which satisfies
all of the given condition, 3<6 and 18%9=0.

Input : N = 15
Output : 4

The basic approach is to iterate using two loops carefully maintaining the given condition 1 <= x < y < N and generate all possible valid pairs and count such pairs for which the product of their values is divisible by sum.
Below is the implementation of the above approach: 

C++

// C++ program to count pairs of numbers
// from 1 to N with Product divisible
// by their Sum

#include <bits/stdc++.h>
using namespace std;

// Function to count pairs
int countPairs(int n)
{
    // variable to store count
    int count = 0;

    // Generate all possible pairs such that
    // 1 <= x < y < n
    for (int x = 1; x < n; x++) {
        for (int y = x + 1; y <= n; y++) {
            if ((y * x) % (y + x) == 0)
                count++;
        }
    }

    return count;
}

// Driver code
int main()
{
    int n = 15;

    cout << countPairs(n);

    return 0;
}

Java

// Java program to count pairs of numbers
// from 1 to N with Product divisible
// by their Sum

import java.io.*;

class GFG {



// Function to count pairs
static int countPairs(int n)
{
    // variable to store count
    int count = 0;

    // Generate all possible pairs such that
    // 1 <= x < y < n
    for (int x = 1; x < n; x++) {
        for (int y = x + 1; y <= n; y++) {
            if ((y * x) % (y + x) == 0)
                count++;
        }
    }

    return count;
}

// Driver code

    public static void main (String[] args) {
            int n = 15;

    System.out.println(countPairs(n));
    }
}
// This code is contributed by anuj_67..

Python3

# Python 3 program to count pairs of numbers
# from 1 to N with Product divisible
# by their Sum

# Function to count pairs
def countPairs(n):

    # variable to store count
    count = 0

    # Generate all possible pairs such that
    # 1 <= x < y < n
    for x in range(1, n):
        for y in range(x + 1, n + 1):
            if ((y * x) % (y + x) == 0):
                count += 1

    return count

# Driver code
n = 15
print(countPairs(n))

# This code is contributed
# by PrinciRaj1992

C#

// C# program to count pairs of numbers
// from 1 to N with Product divisible
// by their Sum
using System;

class GFG
{

// Function to count pairs
static int countPairs(int n)
{
    // variable to store count
    int count = 0;

    // Generate all possible pairs
    // such that 1 <= x < y < n
    for (int x = 1; x < n; x++)
    {
        for (int y = x + 1; y <= n; y++)
        {
            if ((y * x) % (y + x) == 0)
                count++;
        }
    }

    return count;
}

// Driver code
public static void Main ()
{
    int n = 15;

    Console.WriteLine(countPairs(n));
}
}

// This code is contributed by anuj_67

PHP

<?php
// PHP program to count pairs of
// numbers from 1 to N with Product
// divisible by their Sum

// Function to count pairs
function countPairs($n)
{
    // variable to store count
    $count = 0;

    // Generate all possible pairs
    // such that 1 <= x < y < n
    for ($x = 1; $x < $n; $x++)
    {
        for ($y = $x + 1; $y <= $n; $y++)
        {
            if (($y * $x) % ($y + $x) == 0)
                $count++;
        }
    }

    return $count;
}

// Driver code
$n = 15;
echo countPairs($n);

// This code is contributed by ajit
?>

Javascript

<script>
// Javascript program to count pairs of numbers
// from 1 to N with Product divisible
// by their Sum

// Function to count pairs
function countPairs(n)
{
    // variable to store count
    let count = 0;

    // Generate all possible pairs such that
    // 1 <= x < y < n
    for (let x = 1; x < n; x++) {
        for (let y = x + 1; y <= n; y++) {
            if ((y * x) % (y + x) == 0)
                count++;
        }
    }

    return count;
}

// Driver code
let n = 15;

document.write(countPairs(n));

// This code is contributed by souravmahato348.
</script>

Output:

4

Time Complexity : O(N²)

Auxiliary Space: O(1)