Count pairs in an array containing at least one even value
Last Updated :
26 Jul, 2021
Given an array arr[], the task is to count pairs such that each pair (arr[i], arr[j]) contains at least one even element in it where i != j.
Examples:
Input: arr[] = {1, 2, 3, 1, 3}
Output: 4
Explanation:
Possible pairs are: (1, 2), (2, 3), (2, 1), (2, 3).
Input: arr[] = {8, 2, 3, 1, 4, 2}
Output: 14
Explanation:
Possible pairs are: (8, 2), (8, 3), (8, 1), (8, 4), (8, 2), (2, 3), (2, 1), (2, 4), (2, 2), (3, 4), (3, 2), (1, 4), (1, 2), (4, 2).
A Simple Approach is to run two loops. Pick each element one-by-one and for each element find element on right side of array that holds condition, then increment count.
Time Complexity:
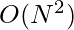
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
int CountPairs(int arr[], int n)
{
int count = 0;
for(int i = 0; i < n; i++)
{
for(int j = i + 1; j < n; j++)
{
if (arr[i] % 2 == 0 ||
arr[j] % 2 == 0)
count++;
}
}
return count;
}
int main()
{
int arr[] = { 8, 2, 3, 1, 4, 2 };
int n = sizeof(arr) / sizeof(int);
cout << (CountPairs(arr, n));
}
|
Java
import java.util.*;
class GFG {
static int CountPairs(int[] arr, int n)
{
int count = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
if (arr[i] % 2 == 0
|| arr[j] % 2 == 0)
count++;
}
}
return count;
}
public static void main(String[] args)
{
int[] arr = { 8, 2, 3, 1, 4, 2 };
int n = arr.length;
System.out.println(CountPairs(arr, n));
}
}
|
Python3
def CountPairs(arr, n):
count = 0
for i in range(n):
for j in range(i + 1, n):
if (arr[i] % 2 == 0 or
arr[j] % 2 == 0):
count += 1
return count
arr = [ 8, 2, 3, 1, 4, 2 ]
n = len(arr)
print(CountPairs(arr, n))
|
C#
using System;
class GFG{
static int CountPairs(int[] arr, int n)
{
int count = 0;
for(int i = 0; i < n; i++)
{
for(int j = i + 1; j < n; j++)
{
if (arr[i] % 2 == 0 ||
arr[j] % 2 == 0)
count++;
}
}
return count;
}
public static void Main(String[] args)
{
int[] arr = { 8, 2, 3, 1, 4, 2 };
int n = arr.Length;
Console.WriteLine(CountPairs(arr, n));
}
}
|
Javascript
<script>
function CountPairs(arr, n)
{
let count = 0;
for(let i = 0; i < n; i++)
{
for(let j = i + 1; j < n; j++)
{
if (arr[i] % 2 == 0 ||
arr[j] % 2 == 0)
count++;
}
}
return count;
}
let arr = [ 8, 2, 3, 1, 4, 2 ];
let n = arr.length;
document.write(CountPairs(arr, n));
</script>
|
Efficient Approach: The idea is to count the even and odd elements in the array and include pairs having only one even element or both the pairs to be even element.
- Pair having exactly one even element: count of the pairs having exactly one even element will be:
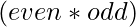
- Pair having exactly two even elements: count of the pairs having exactly two even elements will be:
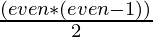
Therefore, the count of the pairs having at least one even element will be
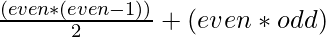
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int CountPairs(int arr[], int n)
{
int even = 0, odd = 0;
for(int i = 0; i < n; i++)
{
if (arr[i] % 2 == 0)
even++;
else
odd++;
}
return (even * (even - 1)) / 2 +
(even * odd);
}
int main()
{
int arr[] = { 8, 2, 3, 1, 4, 2 };
int n = sizeof(arr) / sizeof(int);
cout << CountPairs(arr, n);
}
|
Java
import java.util.*;
class GFG {
static int CountPairs(int[] arr, int n)
{
int even = 0, odd = 0;
for (int i = 0; i < n; i++) {
if (arr[i] % 2 == 0)
even++;
else
odd++;
}
return (even * (even - 1)) / 2
+ (even * odd);
}
public static void main(String[] args)
{
int[] arr = { 8, 2, 3, 1, 4, 2 };
int n = arr.length;
System.out.println(CountPairs(arr, n));
}
}
|
Python3
def CountPairs(arr, n):
even = 0
odd = 0
for i in range(n):
if (arr[i] % 2 == 0):
even += 1
else:
odd += 1
return ((even * (even - 1)) // 2 +
(even * odd))
arr = [ 8, 2, 3, 1, 4, 2 ]
n = len(arr)
print(CountPairs(arr, n))
|
C#
using System;
class GFG{
static int CountPairs(int[] arr, int n)
{
int even = 0, odd = 0;
for(int i = 0; i < n; i++)
{
if (arr[i] % 2 == 0)
even++;
else
odd++;
}
return (even * (even - 1)) / 2 +
(even * odd);
}
public static void Main()
{
int[] arr = { 8, 2, 3, 1, 4, 2 };
int n = arr.Length;
Console.Write(CountPairs(arr, n));
}
}
|
Javascript
<script>
function CountPairs(arr, n)
{
let even = 0, odd = 0;
for(let i = 0; i < n; i++)
{
if (arr[i] % 2 == 0)
even++;
else
odd++;
}
return (even * (even - 1)) / 2 + (even * odd);
}
let arr = [ 8, 2, 3, 1, 4, 2 ];
let n = arr.length;
document.write(CountPairs(arr, n));
</script>
|
Time Complexity: O(N)
Space Complexity: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...