Count pairs from two arrays whose modulo operation yields K
Last Updated :
08 Sep, 2022
Given an integer 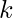 and two arrays
and two arrays 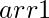 and
and 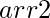 , the task is to count the total pairs (formed after choosing an element from
, the task is to count the total pairs (formed after choosing an element from 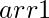 and another from
and another from 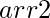 ) from these arrays whose modulo operation yields
) from these arrays whose modulo operation yields 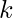 .
.
Note: If in a pair (a, b), a > b then the modulo must be performed as a % b. Also, pairs occurring more than once will be counted only once.
Examples:
Input: arr1[] = {1, 3, 7}, arr2[] = {5, 3, 1}, K = 2
Output: 2
(3, 5) and (7, 5) are the only possible pairs.
Since, 5 % 3 = 2 and 7 % 5 = 2
Input: arr1[] = {2, 5, 99}, arr2[] = {2, 8, 1, 4}, K = 0
Output: 6
All possible pairs are (2, 2), (2, 8), (2, 4), (2, 1), (5, 1) and (99, 1).
Approach:
- Take one element from
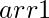 at a time and perform it’s modulo operation with all the other elements of
at a time and perform it’s modulo operation with all the other elements of 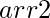 one by one.
one by one. - If the result from the previous step is equal to
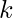 then store the pair (a, b) in a set in order to avoid duplicates where a is the smaller element and b is the larger one.
then store the pair (a, b) in a set in order to avoid duplicates where a is the smaller element and b is the larger one. - Total required pairs will be the size of the set in the end.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int totalPairs(int arr1[], int arr2[], int K, int n, int m)
{
set<pair<int, int> > s;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (arr1[i] > arr2[j]) {
if (arr1[i] % arr2[j] == K)
s.insert(make_pair(arr1[i], arr2[j]));
}
else {
if (arr2[j] % arr1[i] == K)
s.insert(make_pair(arr2[j], arr1[i]));
}
}
}
return s.size();
}
int main()
{
int arr1[] = { 8, 3, 7, 50 };
int arr2[] = { 5, 1, 10, 4 };
int K = 3;
int n = sizeof(arr1) / sizeof(arr1[0]);
int m = sizeof(arr2) / sizeof(arr2[0]);
cout << totalPairs(arr1, arr2, K, n, m);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static class pair
{
int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
static int totalPairs(int []arr1, int []arr2,
int K, int n, int m)
{
HashSet<pair> s = new HashSet<pair>();
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
if (arr1[i] > arr2[j])
{
if (arr1[i] % arr2[j] == K)
s.add(new pair(arr1[i], arr2[j]));
}
else
{
if (arr2[j] % arr1[i] == K)
s.add(new pair(arr2[j], arr1[i]));
}
}
}
return s.size();
}
public static void main(String []args)
{
int []arr1 = { 8, 3, 7, 50 };
int []arr2 = { 5, 1, 10, 4 };
int K = 3;
int n = arr1.length;
int m = arr2.length;
System.out.println(totalPairs(arr1, arr2, K, n, m));
}
}
|
Python3
def totalPairs(arr1, arr2, K, n, m):
s={}
for i in range(n):
for j in range(m):
if (arr1[i] > arr2[j]):
if (arr1[i] % arr2[j] == K):
s[(arr1[i], arr2[j])]=1
else:
if (arr2[j] % arr1[i] == K):
s[(arr2[j], arr1[i])]=1
return len(s)
arr1 = [ 8, 3, 7, 50 ]
arr2 = [5, 1, 10, 4 ]
K = 3
n = len(arr1)
m = len(arr2)
print(totalPairs(arr1, arr2, K, n, m))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
public class pair
{
public int first, second;
public pair(int first, int second)
{
this.first = first;
this.second = second;
}
}
static int totalPairs(int []arr1, int []arr2,
int K, int n, int m)
{
HashSet<pair> s = new HashSet<pair>();
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
if (arr1[i] > arr2[j])
{
if (arr1[i] % arr2[j] == K)
s.Add(new pair(arr1[i], arr2[j]));
}
else
{
if (arr2[j] % arr1[i] == K)
s.Add(new pair(arr2[j], arr1[i]));
}
}
}
return s.Count;
}
public static void Main(String []args)
{
int []arr1 = { 8, 3, 7, 50 };
int []arr2 = { 5, 1, 10, 4 };
int K = 3;
int n = arr1.Length;
int m = arr2.Length;
Console.WriteLine(totalPairs(arr1, arr2, K, n, m));
}
}
|
Javascript
<script>
function totalPairs(arr1, arr2, K, n, m)
{
var s = new Set();
for (var i = 0; i < n; i++) {
for (var j = 0; j < m; j++) {
if (arr1[i] > arr2[j]) {
if (arr1[i] % arr2[j] == K)
s.add([arr1[i], arr2[j]]);
}
else {
if (arr2[j] % arr1[i] == K)
s.add([arr2[j], arr1[i]]);
}
}
}
return s.size;
}
var arr1 = [ 8, 3, 7, 50 ];
var arr2 = [ 5, 1, 10, 4 ];
var K = 3;
var n = arr1.length;
var m = arr2.length;
document.write( totalPairs(arr1, arr2, K, n, m));
</script>
|
Complexity Analysis:
- Time Complexity: O(n * m)
- Auxiliary Space: O(n * m)
Note: To print all the pairs just print the elements of set.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...