Count ordered pairs with product less than N
Last Updated :
25 Jul, 2022
Given an integer N. The task is to count the number of ordered pairs (a, b) such that 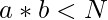 .
.
Examples:
Input: N = 5
Output: 8
Ordered Pairs are = (1, 1), (1, 2), (1, 3),
(1, 4), (2, 1), (2, 2), (3, 1), (4, 1).
Input: N = 1000
Output: 7053
Naive Approach: Run two for loops upto N – 1 and count ordered pairs whose products are less than N.
Efficient Approach: Let’s considered an ordered pair (a, b). Then, if the product of two numbers is less than n i:e a * b < n, then at least one of them must be less than square root of n. We can prove by contradiction that if both numbers are greater than the square root of n then their product is not less than n.
So, you can take all integers up to sqrt(n – 1) instead of all integers up to n. For each a, count the number of b >= a such that a * b < n. Then multiply the result by two to count the pair (b, a) for each pair (a, b) you saw. After that, subtract the integer part of sqrt(n – 1) to ensure the pairs (a, a) were counted exactly once.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countOrderedPairs(int N)
{
int count_pairs = 0;
for (int i = 1; i <= sqrt(N - 1); ++i) {
for (int j = i; j * i < N; ++j)
++count_pairs;
}
count_pairs *= 2;
count_pairs -= int(sqrt(N - 1));
return count_pairs;
}
int main()
{
int N = 5;
cout << countOrderedPairs(N);
return 0;
}
|
Java
class GFG{
static int countOrderedPairs(int N)
{
int count_pairs = 0;
for (int i = 1; i <= (int)Math.sqrt(N - 1); ++i) {
for (int j = i; j * i < N; ++j)
++count_pairs;
}
count_pairs *= 2;
count_pairs -= (int)(Math.sqrt(N - 1));
return count_pairs;
}
public static void main(String[] args)
{
int N = 5;
System.out.println(countOrderedPairs(N));
}
}
|
Python3
from math import sqrt
def countOrderedPairs(N):
count_pairs = 0
p = int(sqrt(N-1)) + 1
q = int(sqrt(N))+2
for i in range(1,p,1):
for j in range(i,q,1):
count_pairs += 1
count_pairs *= 2
count_pairs -= int(sqrt(N - 1))
return count_pairs
if __name__ == '__main__':
N = 5
print(countOrderedPairs(N))
|
C#
using System;
public class GFG{
static int countOrderedPairs(int N)
{
int count_pairs = 0;
for (int i = 1; i <= (int)Math.Sqrt(N - 1); ++i) {
for (int j = i; j * i < N; ++j)
++count_pairs;
}
count_pairs *= 2;
count_pairs -= (int)(Math.Sqrt(N - 1));
return count_pairs;
}
static public void Main (){
int N = 5;
Console.WriteLine(countOrderedPairs(N));
}
}
|
PHP
<?php
function countOrderedPairs($N)
{
$count_pairs = 0;
for ($i = 1; $i <= sqrt($N - 1); ++$i)
{
for ( $j = $i; $j * $i < $N; ++$j)
++$count_pairs;
}
$count_pairs *= 2;
$count_pairs -= (sqrt($N - 1));
return $count_pairs;
}
$N = 5;
echo countOrderedPairs($N);
?>
|
Javascript
<script>
function countOrderedPairs( N)
{
var count_pairs = 0;
for (var i = 1; i <= Math.sqrt(N - 1); ++i) {
for (var j = i; j * i < N; ++j)
++count_pairs;
}
count_pairs *= 2;
count_pairs -= parseInt(Math.sqrt(N - 1));
return count_pairs;
}
var N = 5;
document.write( countOrderedPairs(N));
</script>
|
Time Complexity: O(N*sqrt(N)), Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...