Count operations of the given type required to reduce N to 0
Last Updated :
23 Jun, 2022
Given an integer n. The task is to count the number of operations required to reduce n to 0. In every operation, n can be updated as n = n – d where d is the smallest prime divisor of n.
Examples:
Input: n = 5
Output: 1
5 is the smallest prime divisor, thus it gets subtracted and n gets reduced to 0.
Input: n = 25
Output: 11
5 is the smallest prime divisor, thus it gets subtracted and n gets reduced to 20. Then 2 is the smallest divisor and so on.
Input: n = 4
Output: 2
Approach:
- When n is even then the smallest prime divisor of n will be 2 and subtracting 2 from n will again give an even integer i.e. gain 2 will be chosen as the smallest prime divisor and these steps will repeat until n gets reduced to 0.
- When n is odd then the smallest prime divisor of n will also be odd and subtracting an odd integer from another odd integer will give an even integer as the result and then the result can be found out by repeating step 1 for the current even integer.
- Thus, the task is to find the smallest divisor d, subtract it, n = n – d and print 1 + ((n – d) / 2).
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
int countOperations (int n)
{
int i = 2;
while ((i * i) < n && (n % i))
i += 1;
if ((i * i) > n)
i = n;
return (1 + (n - i)/2);
}
int main()
{
int n = 5;
cout << countOperations(n);
}
|
Java
class GFG
{
static int countOperations (int n)
{
int i = 2;
while ((i * i) < n && (n % i) > 0)
i += 1;
if ((i * i) > n)
i = n;
return (1 + (n - i) / 2);
}
public static void main(String[] args)
{
int n = 5;
System.out.println(countOperations(n));
}
}
|
Python3
def countOperations(n):
i = 2
while ((i * i) < n and (n % i)):
i += 1
if ((i * i) > n):
i = n
return (1 + (n - i)//2)
n = 5
print(countOperations(n))
|
C#
using System;
class GFG
{
static int countOperations (int n)
{
int i = 2;
while ((i * i) < n && (n % i) > 0)
i += 1;
if ((i * i) > n)
i = n;
return (1 + (n - i) / 2);
}
static void Main()
{
int n = 5;
Console.WriteLine(countOperations(n));
}
}
|
PHP
<?php
function countOperations($n)
{
$i = 2;
# Finding the smallest divisor
while (($i * $i) < $n and ($n % $i))
$i += 1;
if (($i * $i) > $n)
$i = $n;
# Return the count of operations
return 1 + floor(($n - $i) / 2);
}
$n = 5 ;
echo countOperations($n);
?>
|
Javascript
<script>
function countOperations (n)
{
var i = 2;
while ((i * i) < n && (n % i))
i += 1;
if ((i * i) > n)
i = n;
return (1 + (n - i)/2);
}
var n = 5;
document.write( countOperations(n))
</script>
|
Time Complexity: 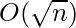
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...