Count of ways to represent N as sum of a prime number and twice of a square
Last Updated :
14 Feb, 2023
Given an integer N, the task is to count the number of ways so that N can be written as the sum of a prime number and twice of a square, i.e.
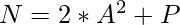
, where P can be any prime number and A is any positive integer.
Note:
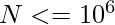
Examples:
Input: N = 9
Output: 1
Explanation:
9 can be represented as sum of prime number and twice a square in only one way –
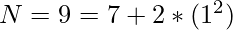
Input: N = 15
Output: 2
Explanation:
15 can be represented as sum of prime number and twice a square in two ways –
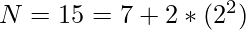 [Tex]N = 15 = 13 + 2 * (1^{2}) [/Tex]
[Tex]N = 15 = 13 + 2 * (1^{2}) [/Tex]
Approach: The idea is to use Sieve of Eratosthenes to find all the primes and then for each prime number check for every possible number starting from 1. If any prime number and twice a square is equal to the given number then increment the count of the number of ways by 1.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
long long int n = 500000 - 2;
vector<long long int> v;
void sieveoferanthones()
{
bool prime[n + 1];
memset(prime, true, sizeof(prime));
for (long long int i = 2; i <= sqrt(n); i++) {
if (prime[i])
for (long long int j = i * i; j <= n; j += i) {
prime[j] = false;
}
}
for (long long int i = 2; i < n; i++) {
if (prime[i])
v.push_back(i);
}
}
void numberOfWays(long long int n)
{
long long int count = 0;
for (long long int j = 1; 2 * (pow(j, 2)) < n; j++) {
for (long long int i = 1; v[i] + 2 <= n; i++) {
if (n == v[i] + (2 * (pow(j, 2))))
count++;
}
}
cout << count << endl;
}
int main()
{
sieveoferanthones();
long long int n = 9;
numberOfWays(n);
return 0;
}
|
Java
import java.util.*;
class GFG {
static int n = 500000 - 2;
static Vector<Integer> v = new Vector<>();
static void sieveoferanthones()
{
boolean[] prime = new boolean[n + 1];
Arrays.fill(prime, true);
for (int i = 2; i <= Math.sqrt(n); i++) {
if (prime[i])
for (int j = i * i; j <= n; j += i) {
prime[j] = false;
}
}
for (int i = 2; i < n; i++) {
if (prime[i])
v.add(i);
}
}
static void numberOfWays(int n)
{
int count = 0;
for (int j = 1; 2 * (Math.pow(j, 2)) < n; j++) {
for (int i = 1; v.get(i) + 2 <= n; i++) {
if (n == v.get(i) + (2 * (Math.pow(j, 2))))
count++;
}
}
System.out.print(count + "\n");
}
public static void main(String[] args)
{
sieveoferanthones();
int n = 9;
numberOfWays(n);
}
}
|
Python3
import math
n = 500000 - 2
v = []
def sieveoferanthones():
prime = [1] * (n + 1)
for i in range(2, int(math.sqrt(n)) + 1):
if (prime[i] != 0):
for j in range(i * i, n + 1, i):
prime[j] = False
for i in range(2, n):
if (prime[i] != 0):
v.append(i)
def numberOfWays(n):
count = 0
j = 1
while (2 * (pow(j, 2)) < n):
i = 1
while (v[i] + 2 <= n):
if (n == v[i] +
(2 * (math.pow(j, 2)))):
count += 1
i += 1
j += 1
print(count)
sieveoferanthones()
n = 9
numberOfWays(n)
|
C#
using System;
using System.Collections;
using System.Collections.Generic;
class GFG {
static int n = 500000 - 2;
static ArrayList v = new ArrayList();
static void sieveoferanthones()
{
bool[] prime = new bool[n + 1];
Array.Fill(prime, true);
for (int i = 2; i <= (int)Math.Sqrt(n); i++) {
if (prime[i]) {
for (int j = i * i; j <= n; j += i) {
prime[j] = false;
}
}
}
for (int i = 2; i < n; i++) {
if (prime[i])
v.Add(i);
}
}
static void numberOfWays(int n)
{
int count = 0;
for (int j = 1; 2 * (Math.Pow(j, 2)) < n; j++) {
for (int i = 1; (int)v[i] + 2 <= n; i++) {
if (n == (int)v[i] + (2 * (Math.Pow(j, 2))))
count++;
}
}
Console.Write(count);
}
public static void Main(string[] args)
{
sieveoferanthones();
int n = 9;
numberOfWays(n);
}
}
|
Javascript
<script>
let n = 500000 - 2;
let v = [];
function sieveoferanthones()
{
let prime = Array.from({length: n+1},
(_, i) => true);
for (let i = 2;
i <= Math.sqrt(n); i++)
{
if (prime[i])
for (let j = i * i;
j <= n; j += i)
{
prime[j] = false;
}
}
for (let i = 2; i < n; i++)
{
if (prime[i])
v.push(i);
}
}
function numberOfWays(n)
{
let count = 0;
for (let j = 1; 2 *
(Math.pow(j, 2)) < n; j++)
{
for (let i = 1; v[i] +
2 <= n; i++)
{
if (n == v[i] +
(2 * (Math.pow(j, 2))))
count++;
}
}
document.write(count + "<br/>");
}
sieveoferanthones();
let N = 9;
numberOfWays(N);
</script>
|
Time Complexity: O(n2)
Auxiliary Space: O(n)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...