Count of ways to choose N people containing at least 4 boys and 1 girl from P boys and Q girls
Last Updated :
02 Feb, 2022
Given integers N, P, and Q the task is to find the number of ways to form a group of N people having at least 4 boys and 1 girls from P boys and Q girls.
Examples:
Input: P = 5, Q = 2, N = 5
Output: 10
Explanation: Suppose given pool is {m1, m2, m3, m4, m5} and {w1, w2}. Then possible combinations are:
m1 m2 m3 m4 w1
m2 m3 m4 m5 w1
m1 m3 m4 m5 w1
m1 m2 m4 m5 w1
m1 m2 m3 m5 w1
m1 m2 m3 m4 w2
m2 m3 m4 m5 w2
m1 m3 m4 m5 w2
m1 m2 m4 m5 w2
m1 m2 m3 m5 w2
Hence the count is 10.
Input: P = 5, Q = 2, N = 6
Output: 7
Approach: This problem is based on combinatorics where we need to select at least 4 boys out of 1 boys available, and at least Y girls out of Q girls available, so that total people selected are N.
Consider the example:
P = 5, Q = 2, N = 6
In this, the possible selections are:
(4 boys out of 5) * (2 girls out of 2) + (5 boys out of 5) * (1 girl out of 2)
= 5C4 * 2C2 + 5C5 * 2C1
So for some general values of P, Q and N, the approach can be visualised as:

where

Follow the steps mentioned below to implementation it:
- Start iterating a loop from i = 4 till i = P.
- At each iteration calculate the number of possible ways if we choose i boys and (N-i) girls, using combination
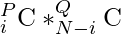
- Add the possible value for each iteration as the total number of ways.
- Return the total calculated ways at the end.
Below is the implementation of the approach:
C++
#include <bits/stdc++.h>
using namespace std;
long long int fact(int f)
{
f++;
long long int ans = 1;
while (--f > 0)
ans = ans * f;
return ans;
}
long long int ncr(int n, int r)
{
return (fact(n) / (fact(r) * fact(n - r)));
}
long long int countWays(int n, int p, int q)
{
long long int sum = 0;
for (long long int i = 4; i <= p; i++) {
if (n - i >= 1 && n - i <= q)
sum += (ncr(p, i) * ncr(q, n - i));
}
return sum;
}
int main()
{
int P = 5, Q = 2, N = 5;
cout << countWays(N, P, Q) << endl;
return 0;
}
|
Java
import java.util.*;
class GFG{
static int fact(int f)
{
f++;
int ans = 1;
while (--f > 0)
ans = ans * f;
return ans;
}
static int ncr(int n, int r)
{
return (fact(n) / (fact(r) * fact(n - r)));
}
static int countWays(int n, int p, int q)
{
int sum = 0;
for (int i = 4; i <= p; i++) {
if (n - i >= 1 && n - i <= q)
sum += (ncr(p, i) * ncr(q, n - i));
}
return sum;
}
public static void main(String[] args)
{
int P = 5, Q = 2, N = 5;
System.out.print(countWays(N, P, Q) +"\n");
}
}
|
Python3
def fact(f):
ans = 1
while (f):
ans = ans * f
f -= 1
return ans
def ncr(n, r):
return (fact(n) / (fact(r) * fact(n - r)))
def countWays(n, p, q):
sum = 0
for i in range(4, p + 1):
if (n - i >= 1 and n - i <= q):
sum += (ncr(p, i) * ncr(q, n - i))
return (int)(sum)
P = 5
Q = 2
N = 5
print(countWays(N, P, Q))
|
C#
using System;
using System.Collections.Generic;
class GFG {
static int fact(int f)
{
f++;
int ans = 1;
while (--f > 0)
ans = ans * f;
return ans;
}
static int ncr(int n, int r)
{
return (fact(n) / (fact(r) * fact(n - r)));
}
static int countWays(int n, int p, int q)
{
int sum = 0;
for (int i = 4; i <= p; i++) {
if (n - i >= 1 && n - i <= q)
sum += (ncr(p, i) * ncr(q, n - i));
}
return sum;
}
public static void Main()
{
int P = 5, Q = 2, N = 5;
Console.Write(countWays(N, P, Q));
}
}
|
Javascript
<script>
const fact = (f) => {
f++;
let ans = 1;
while (--f > 0)
ans = ans * f;
return ans;
}
const ncr = (n, r) => {
return (fact(n) / (fact(r) * fact(n - r)));
}
const countWays = (n, p, q) => {
let sum = 0;
for (let i = 4; i <= p; i++) {
if (n - i >= 1 && n - i <= q)
sum += (ncr(p, i) * ncr(q, n - i));
}
return sum;
}
let P = 5, Q = 2, N = 5;
document.write(countWays(N, P, Q));
</script>
|
Time Complexity: O(N2)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...