Count of triples (A, B, C) where A*C is greater than B*B
Last Updated :
09 Sep, 2022
Given three integers A, B and C. The task is to count the number of triples (a, b, c) such that a * c > b2, where 0 < a <= A, 0 < b <= B and 0 < c <= C.
Examples:
Input: A = 3, B = 2, C = 2
Output: 6
Following triples are counted :
(1, 1, 2), (2, 1, 1), (2, 1, 2), (3, 1, 1), (3, 1, 2) and (3, 2, 2).
Input: A = 3, B = 3, C = 3
Output: 11
Naive approach:
The brute force approach is to consider all possible triples (a, b, c) and count those triples that satisfy the constraint a*c > b2.
Below is the implementation of the given approach.
C++
#include <bits/stdc++.h>
using namespace std;
long long countTriplets(int A, int B, int C)
{
long long ans = 0;
for (int i = 1; i <= A; i++) {
for (int j = 1; j <= B; j++) {
for (int k = 1; k <= C; k++) {
if (i * k > j * j)
ans++;
}
}
}
return ans;
}
int main()
{
int A, B, C;
A = 3, B = 2, C = 2;
cout << countTriplets(A, B, C);
}
|
Java
import java.util.*;
class GFG
{
static long countTriplets(int A, int B, int C)
{
long ans = 0;
for (int i = 1; i <= A; i++)
{
for (int j = 1; j <= B; j++)
{
for (int k = 1; k <= C; k++)
{
if (i * k > j * j)
ans++;
}
}
}
return ans;
}
public static void main (String[] args)
{
int A = 3, B = 2, C = 2;
System.out.println(countTriplets(A, B, C));
}
}
|
Python3
def countTriplets(A, B, C):
ans = 0
for i in range(1, A + 1):
for j in range(1, B + 1):
for k in range(1, C + 1):
if (i * k > j * j):
ans += 1
return ans
A = 3
B = 2
C = 2
print(countTriplets(A, B, C))
|
C#
using System;
class GFG
{
static long countTriplets(int A,
int B, int C)
{
long ans = 0;
for (int i = 1; i <= A; i++)
{
for (int j = 1; j <= B; j++)
{
for (int k = 1; k <= C; k++)
{
if (i * k > j * j)
ans++;
}
}
}
return ans;
}
public static void Main (String[] args)
{
int A = 3, B = 2, C = 2;
Console.WriteLine(countTriplets(A, B, C));
}
}
|
Javascript
<script>
function countTriplets(A, B, C)
{
let ans = 0;
for (let i = 1; i <= A; i++) {
for (let j = 1; j <= B; j++) {
for (let k = 1; k <= C; k++) {
if (i * k > j * j)
ans++;
}
}
}
return ans;
}
let A, B, C;
A = 3, B = 2, C = 2;
document.write(countTriplets(A, B, C));
</script>
|
Time Complexity: 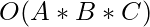 since three nested loops are used the time taken by the algorithm to complete all operations is O(A*B*C).
since three nested loops are used the time taken by the algorithm to complete all operations is O(A*B*C).
Auxiliary Space: O(1), since no extra array is used so the space taken by the algorithm is constant
Efficient approach:
Let us count all triplets for a given value of b = k for all k from 1 to B.
- For a given b = k we need to find all a = i and c = j that satisfy i * j > k2
- For a = i, find smallest c = j that satisfies the condition.
Since c = j satisfies this condition therefore c = j + 1, c = j + 2, … and so on, will also satisfy the condition.
So we can easily count all triples in which a = i and b = k. - Also if for some a = i, c = j is the smallest value such that the given condition is satisfied so it can be observed that a = j and all c >= i also satisfy the condition.
The condition is also satisfied by a = j + 1 and c >= i that is all values a >= j and c >= i also satisfy the condition. - The above observation helps us to count all triples in which b = k and a >= j easily.
- Now we need to count all triples in which b = k and i < a < j.
- Thus for a given value of b = k we only need to go upto a = square root of k.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
long long getCount(int A, int B2,
int C)
{
long long count = 0;
for (int i = 1; i <= A; i++) {
long long j = (B2 / i) + 1;
if (C >= j)
count = (count + C - j + 1);
if (A >= j && C >= i)
count = (count
+ (C - i + 1)
* (A - j + 1));
if (A >= j)
A = j - 1;
}
return count;
}
long long countTriplets(int A, int B,
int C)
{
long long ans = 0;
for (int i = 1; i <= B; i++) {
ans = (ans
+ getCount(A, i * i, C));
}
return ans;
}
int main()
{
int A, B, C;
A = 3, B = 2, C = 2;
cout << countTriplets(A, B, C);
}
|
Java
import java.util.*;
class GFG
{
static long getCount(int A, int B2, int C)
{
long count = 0;
for (int i = 1; i <= A; i++)
{
long j = (B2 / i) + 1;
if (C >= j)
count = (count + C - j + 1);
if (A >= j && C >= i)
count = (count + (C - i + 1) *
(A - j + 1));
if (A >= j)
A = (int) (j - 1);
}
return count;
}
static long countTriplets(int A, int B, int C)
{
long ans = 0;
for (int i = 1; i <= B; i++)
{
ans = (ans + getCount(A, i * i, C));
}
return ans;
}
public static void main(String[] args)
{
int A, B, C;
A = 3; B = 2; C = 2;
System.out.println(countTriplets(A, B, C));
}
}
|
Python3
def getCount(A, B2, C):
count = 0
i=1
while(i<A):
j = (B2 // i) + 1
if (C >= j):
count = count + C - j + 1
if (A>= j and C >= i):
count = count+ (C - i + 1) * (A - j + 1)
if (A >= j):
A = j - 1
i+=1
return count
def countTriplets(A, B, C):
ans = 0
for i in range(1,B+1):
ans = (ans+ getCount(A, i * i, C))
return ans
A = 3
B = 2
C = 2
print(countTriplets(A, B, C))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static long getCount(int A, int B2, int C)
{
long count = 0;
for (int i = 1; i <= A; i++)
{
long j = (B2 / i) + 1;
if (C >= j)
count = (count + C - j + 1);
if (A >= j && C >= i)
count = (count + (C - i + 1) *
(A - j + 1));
if (A >= j)
A = (int) (j - 1);
}
return count;
}
static long countTriplets(int A, int B, int C)
{
long ans = 0;
for (int i = 1; i <= B; i++)
{
ans = (ans + getCount(A, i * i, C));
}
return ans;
}
public static void Main(String[] args)
{
int A, B, C;
A = 3; B = 2; C = 2;
Console.WriteLine(countTriplets(A, B, C));
}
}
|
Javascript
<script>
function getCount(A, B2, C)
{
let count = 0;
for (let i = 1; i <= A; i++) {
let j = parseInt(B2 / i) + 1;
if (C >= j)
count = (count + C - j + 1);
if (A >= j && C >= i)
count = (count
+ (C - i + 1)
* (A - j + 1));
if (A >= j)
A = j - 1;
}
return count;
}
function countTriplets(A, B, )
{
let ans = 0;
for (let i = 1; i <= B; i++) {
ans = (ans
+ getCount(A, i * i, C));
}
return ans;
}
let A, B, C;
A = 3, B = 2, C = 2;
document.write(countTriplets(A, B, C));
</script>
|
Time Complexity: O(A*B), since two nested loops are used the time taken by the algorithm to complete all operations is O(A*B).
Auxiliary Space: O(1), since no extra array is used so the space taken by the algorithm is constant
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...