Count of subsequences which consists exactly K prime numbers
Last Updated :
31 Aug, 2022
Given an integer K and an array arr[], the task is to find the number of subsequences from the given array such that each subsequence consists exactly K prime numbers.
Example:
Input: K = 2, arr = [2, 3, 4, 6]
Output: 4
Explanation:
There are 4 subsequences which consists exactly 2 prime numbers {2, 3} {2, 3, 4} {2, 3, 6} {2, 3, 4, 6}
Input: K = 3, arr = [1, 2, 3, 4, 5, 6, 7]
Output: 32
Explanation:
There are 32 subsequences which consists exactly 3 prime numbers.
Approach: To solve the problem mentioned above we have to find the count of prime numbers in the given array.
- Let the count of prime numbers is m.
- We can choose any K integers among m prime numbers.
- So the possible combination of choosing prime numbers in the subsequence is
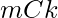 and in the subsequence we can add any number of non – prime numbers because there is no restriction on the non prime numbers where count of non prime numbers will be (N – m).
and in the subsequence we can add any number of non – prime numbers because there is no restriction on the non prime numbers where count of non prime numbers will be (N – m). - We can choose any subset of the (N – m) for nonprime numbers in our subsequence.
- Possibility of choosing all subset of size (N – m) is pow(2, (m – N)).
- For generating subsequences, we will multiply prime number possibility with nonprime number possibility.
Sub sequence count = (Count of prime numbers) C (K) * pow(2, count of non-prime numbers)
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int fact(int n)
{
int res = 1;
for (int i = 2; i <= n; i++)
res = res * i;
return res;
}
int nCr(int n, int r)
{
return fact(n)
/ (fact(r)
* fact(n - r));
}
bool isPrime(int n)
{
if (n <= 1)
return false;
for (int i = 2; i < n; i++)
if (n % i == 0)
return false;
return true;
}
int countSubsequences(int arr[], int n, int k)
{
int countPrime = 0;
for (int i = 0; i < n; i++) {
if (isPrime(arr[i]))
countPrime++;
}
if (countPrime < k)
return 0;
return nCr(countPrime, k)
* pow(2, (n - countPrime));
}
int main()
{
int arr[] = { 1, 2, 3, 4, 5, 6, 7 };
int K = 3;
int n = sizeof(arr) / sizeof(arr[0]);
cout << countSubsequences(arr, n, K);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int fact(int n)
{
int res = 1;
for(int i = 2; i <= n; i++)
res = res * i;
return res;
}
static int nCr(int n, int r)
{
return fact(n) / (fact(r) *
fact(n - r));
}
static boolean isPrime(int n)
{
if (n <= 1)
return false;
for(int i = 2; i < n; i++)
if (n % i == 0)
return false;
return true;
}
static int countSubsequences(int arr[],
int n, int k)
{
int countPrime = 0;
for(int i = 0; i < n; i++)
{
if (isPrime(arr[i]))
countPrime++;
}
if (countPrime < k)
return 0;
return nCr(countPrime, k) *
(int)Math.pow(2, (n - countPrime));
}
public static void main(String args[])
{
int arr[] = { 1, 2, 3, 4, 5, 6, 7 };
int K = 3;
int n = arr.length;
System.out.println(countSubsequences(arr, n, K));
}
}
|
Python3
def fact(n):
res = 1;
for i in range(2, n + 1):
res = res * i
return res
def nCr(n, r):
return (fact(n) // (fact(r) *
fact(n - r)))
def isPrime(n):
if (n <= 1):
return False;
for i in range(2, n):
if (n % i == 0):
return False
return True
def countSubsequences(arr, n, k):
countPrime = 0
for i in range(n):
if (isPrime(arr[i])):
countPrime += 1
if (countPrime < k):
return 0
return (nCr(countPrime, k) *
pow(2, (n - countPrime)))
arr = [ 1, 2, 3, 4, 5, 6, 7 ]
K = 3
n = len(arr)
print(countSubsequences(arr, n, K))
|
C#
using System;
class GFG{
static int fact(int n)
{
int res = 1;
for(int i = 2; i <= n; i++)
res = res * i;
return res;
}
static int nCr(int n, int r)
{
return fact(n) / (fact(r) *
fact(n - r));
}
static bool isPrime(int n)
{
if (n <= 1)
return false;
for(int i = 2; i < n; i++)
if (n % i == 0)
return false;
return true;
}
static int countSubsequences(int []arr,
int n, int k)
{
int countPrime = 0;
for(int i = 0; i < n; i++)
{
if (isPrime(arr[i]))
countPrime++;
}
if (countPrime < k)
return 0;
return nCr(countPrime, k) *
(int)Math.Pow(2, (n - countPrime));
}
public static void Main(String []args)
{
int []arr = { 1, 2, 3, 4, 5, 6, 7 };
int K = 3;
int n = arr.Length;
Console.WriteLine(countSubsequences(arr, n, K));
}
}
|
Javascript
<script>
function fact(n)
{
var res = 1;
for (var i = 2; i <= n; i++)
res = res * i;
return res;
}
function nCr(n, r)
{
return fact(n)
/ (fact(r)
* fact(n - r));
}
function isPrime(n)
{
if (n <= 1)
return false;
for (var i = 2; i < n; i++)
if (n % i == 0)
return false;
return true;
}
function countSubsequences(arr, n, k)
{
var countPrime = 0;
for (var i = 0; i < n; i++) {
if (isPrime(arr[i]))
countPrime++;
}
if (countPrime < k)
return 0;
return nCr(countPrime, k)
* Math.pow(2, (n - countPrime));
}
var arr = [ 1, 2, 3, 4, 5, 6, 7 ];
var K = 3;
var n = arr.length;
document.write( countSubsequences(arr, n, K));
</script>
|
Time Complexity: O(N^2) .
Auxiliary Space: O(1) .
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...