Count of root to leaf paths in a Binary Tree that form an AP
Last Updated :
23 Aug, 2021
Given a Binary Tree, the task is to count all paths from root to leaf which forms an Arithmetic Progression.
Examples:
Input:
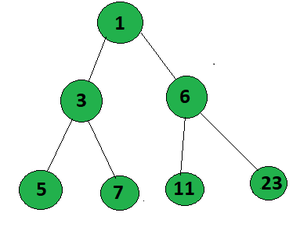
Output: 2
Explanation:
The paths that form an AP in the given tree from root to leaf are:
- 1->3->5 (A.P. with common difference 2)
- 1->6->11 (A.P. with common difference 5)
Input:
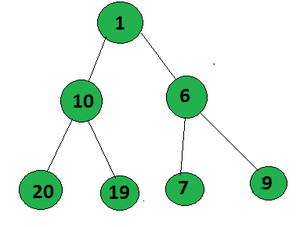
Output: 1
Explanation:
The path that form an AP in the given tree from root to leaf is 1->10->19 (A.P. with difference 9)
Approach: The problem can be solved using the Preorder Traversal. Follow the steps below to solve the problem:
- Perform Preorder Traversal on the given binary tree.
- Initialize an array arr[] to store the path.
- Initialize count = 0, to store the count of paths which forms an A.P.
- After reaching the leaf node, check if the current elements in the array(i.e. the node values from root to leaf path) forms an A.P..
- If so, increment the count
- After the complete traversal of the tree, print the count.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int count = 0;
struct Node {
int val;
Node *left, *right;
Node(int x)
{
val = x;
left = NULL;
right = NULL;
}
};
bool check(vector<int> arr)
{
if (arr.size() == 1)
return true;
int d = arr[1] - arr[0];
for (int i = 2; i < arr.size(); i++) {
if (arr[i] - arr[i - 1] != d)
return false;
}
return true;
}
int countAP(Node* root, vector<int> arr)
{
if (!root)
return 0;
arr.push_back(root->val);
if (root->left == NULL
&& root->right == NULL) {
if (check(arr))
return 1;
return 0;
}
int x = countAP(root->left, arr);
int y = countAP(root->right, arr);
return x + y;
}
int main()
{
Node* root = new Node(1);
root->left = new Node(3);
root->right = new Node(6);
root->left->left = new Node(5);
root->left->right = new Node(7);
root->right->left = new Node(11);
root->right->right = new Node(23);
cout << countAP(root, {});
return 0;
}
|
Java
import java.util.*;
class GFG{
int count = 0;
static class Node
{
int val;
Node left, right;
Node(int x)
{
val = x;
left = null;
right = null;
}
};
static boolean check(Vector<Integer> arr)
{
if (arr.size() == 1)
return true;
int d = arr.get(1) - arr.get(0);
for(int i = 2; i < arr.size(); i++)
{
if (arr.get(i) - arr.get(i - 1) != d)
return false;
}
return true;
}
static int countAP(Node root,
Vector<Integer> arr)
{
if (root == null)
return 0;
arr.add(root.val);
if (root.left == null &&
root.right == null)
{
if (check(arr))
return 1;
return 0;
}
int x = countAP(root.left, arr);
int y = countAP(root.right, arr);
return x + y;
}
public static void main(String[] args)
{
Node root = new Node(1);
root.left = new Node(3);
root.right = new Node(6);
root.left.left = new Node(5);
root.left.right = new Node(7);
root.right.left = new Node(11);
root.right.right = new Node(23);
System.out.print(countAP(root, new Vector<Integer>()));
}
}
|
Python3
class Node:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def check(arr):
if len(arr) == 1:
return True
d = arr[1] - arr[0]
for i in range(2, len(arr)):
if arr[i] - arr[i - 1] != d:
return False
return True
def countAP(root, arr):
if not root:
return 0
arr.append(root.val)
if (root.left == None and
root.right == None):
if check(arr):
return 1
return 0
x = countAP(root.left, arr)
y = countAP(root.right, arr)
return x + y
root = Node(1)
root.left = Node(3)
root.right = Node(6)
root.left.left = Node(5)
root.left.right = Node(7)
root.right.left = Node(11)
root.right.right = Node(23)
print(countAP(root, []))
|
C#
using System;
using System.Collections.Generic;
class GFG{
class Node
{
public int val;
public Node left, right;
public Node(int x)
{
val = x;
left = null;
right = null;
}
};
static bool check(List<int> arr)
{
if (arr.Count == 1)
return true;
int d = arr[1] - arr[0];
for(int i = 2; i < arr.Count; i++)
{
if (arr[i] - arr[i - 1] != d)
return false;
}
return true;
}
static int countAP(Node root,
List<int> arr)
{
if (root == null)
return 0;
arr.Add(root.val);
if (root.left == null &&
root.right == null)
{
if (check(arr))
return 1;
return 0;
}
int x = countAP(root.left, arr);
int y = countAP(root.right, arr);
return x + y;
}
public static void Main(String[] args)
{
Node root = new Node(1);
root.left = new Node(3);
root.right = new Node(6);
root.left.left = new Node(5);
root.left.right = new Node(7);
root.right.left = new Node(11);
root.right.right = new Node(23);
Console.Write(countAP(root, new List<int>()));
}
}
|
Javascript
<script>
let count = 0;
class Node
{
constructor(x)
{
this.val = x;
this.left = null;
this.right = null;
}
}
var root;
function check(arr)
{
if (arr.length == 1)
return true;
let d = arr[1] - arr[0];
for(let i = 2; i < arr.length; i++)
{
if (arr[i] - arr[i - 1] != d)
return false;
}
return true;
}
function countAP(root, arr)
{
if (!root)
return 0;
arr.push(root.val);
if (root.left == null &&
root.right == null)
{
if (check(arr))
return 1;
return 0;
}
let x = countAP(root.left, arr);
let y = countAP(root.right, arr);
return x + y;
}
root = new Node(1);
root.left = new Node(3);
root.right = new Node(6);
root.left.left = new Node(5);
root.left.right = new Node(7);
root.right.left = new Node(11);
root.right.right = new Node(23);
let arr = [];
document.write(countAP(root, arr));
</script>
|
Output:
2
Time Complexity: O(N)
Auxiliary Space: O(h), where h is the height of binary tree.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...