Count of permutations of an Array having maximum MEXs sum of prefix arrays
Last Updated :
08 Dec, 2021
Given an array arr of size N, the task is to find the number of its permutations such that the sum of MEXs of its prefix arrays is maximum.
Note: MEX of a set of integers is defined as the smallest non-negative integer that does not belong to this set.
Example:
Input: arr[] = {1, 0, 1}
Output: 2
Explanation:
All permutations and their MEXs are as follows:
[0, 1, 2] => array : {1, 0, 1}, MEX({1}) + MEX({1, 0}) + MEX({1, 0, 1}) = 0 + 2 + 2 = 4
[0, 2, 1] => array : {1, 1, 0}, MEX({1}) + MEX({1, 1}) + MEX({1, 1, 0}) = 0 + 0 + 2 = 2
[1, 0, 2] => array : {0, 1, 1}, MEX({0}) + MEX({0, 1}) + MEX({0, 1, 1}) = 1 + 2 + 2 = 5
[1, 2, 0] => array : {0, 1, 1}, MEX({0}) + MEX({0, 1}) + MEX({0, 1, 1}) = 1 + 2 + 2 = 5
[2, 0, 1] => array : {1, 1, 0}, MEX({1}) + MEX({1, 1}) + MEX({1, 1, 0}) = 0 + 0 + 2 = 2
[2, 1, 0] => array : {1, 0, 1}, MEX({1}) + MEX({1, 0}) + MEX({1, 0, 1}) = 0 + 2 + 2 = 4
Hence the maximum sum is 5 and the number of permutations with this sum are 2.
Input: arr[] = {0, 1, 2, 2, 5, 6}
Output: 12
Approach:
The optimal idea is based on the observation that the sum of MEX of prefix arrays will be maximum when all the distinct elements are arranged in increasing order and the duplicates are present at the end of the array (like 0, 1, 2, 3, …). Once this continuity breaks, the MEX of the rest, after that point remains the same. For example in {0, 1, 2, 2, 5, 6} the MEXs of prefix arrays are {1, 2, 3, 3, 3, 3} in which the continuity breaks at index 3.
Now, to find the count of all permutations with maximum MEXs sum, store the frequency of elements in a map. In a maximum MEX prefix array, the first position is always be filled by 0, and then second by 1, then third by 2 and so on. So try to fill these with the number of choices available and once the point where the continuity breaks is reached, the MEX of all permutations after that point is the same and the elements after this can be arranged in any possible permutation. Now to understand it better, let’s say that there are 0 to Y numbers present in the array then continuity breaks and after that K more elements are present. Then the count of permutations with maximum MEXs sum is:
ans = frequency[0] * frequency[1] * frequency[2] * … * frequency[Y] * factorial[K]
Now, in the case of {0, 1, 2, 2, 5, 6}, the array having the maximum sum of MEXs of its prefix arrays can:
- Only contain 0 at index 0, so the number of choices for the first index is 1.
- Only contain 1 at index 1, so the number of choices here is 1.
- Contain any of the two 2’s present, so the number of choices here is 2.
- Now after this the continuity breaks and the elements after this can be arranged in any order:
- So, the total number of choices after this point is
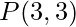 , i.e.
, i.e. 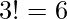 .
.
- Now, the final number of all permutations is
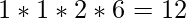 .
.
Follow the steps below to solve the problem:
- Declare a map mp to store the frequency of the elements.
- Now create a variable cnt to keep track of the elements present to the right of an element and initialise it with N i.e. total number of elements present.
- Also declare a variable ans to store the answer and initialize it with 1.
- Now start iterating from 0 up to the size of the given array i.e. from i = 0 to i < n :
- If mp[i] != 0, this means the continuity prevails till this point and all possible choices (i.e. mp[i]) is to be considered. So, ans will become ans=ans*mp[i] and reduce cnt by 1 to get the elements present to the right of the next element.
- If mp[i] == 0, this means that here the continuity breaks and elements after this can be arranged in any possible permutation. So, breaks the loop here and considered all the permutations possible for the elements present to the right of this point, i.e. factorial of cnt.
- Print the answer according to the above observation.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int factorial(int n)
{
int res = 1, i;
for (i = 2; i <= n; i++) {
res *= i;
}
return res;
}
int countPermutations(int ar[], int n)
{
unordered_map<int, int> mp;
int ans = 1, cnt = n;
for (int i = 0; i < n; i++) {
mp[ar[i]]++;
}
for (int i = 0; i < n; i++) {
if (mp[i] == 0) {
break;
}
ans = (ans * mp[i]);
cnt--;
}
ans = ans * factorial(cnt);
return ans;
}
int main()
{
int arr[] = { 1, 0, 1 };
int N = sizeof(arr) / sizeof(arr[0]);
cout << countPermutations(arr, N);
}
|
Java
import java.util.*;
class GFG
{
static int factorial(int n)
{
int res = 1, i;
for (i = 2; i <= n; i++) {
res *= i;
}
return res;
}
static int countPermutations(int[] ar, int n)
{
Map<Integer, Integer> mp= new HashMap<Integer, Integer>();
int ans = 1, cnt = n, i;
for (i = 0; i < n; i++) {
if (mp.containsKey(ar[i]))
{
mp.put(ar[i],mp.get(ar[i])+1);
}
else
{
mp.put(ar[i], 1);
}
}
for (i = 0; i < n; i++) {
if (! mp.containsKey(i)) {
break;
}
ans = (ans * mp.get(i));
cnt--;
}
ans = ans * factorial(cnt);
return ans;
}
public static void main(String[] args)
{
int[] arr = { 1, 0, 1 };
int N = arr.length;
System.out.print(countPermutations(arr, N));
}
}
|
Python3
def factorial(n):
res = 1
for i in range(2, n + 1):
res *= i
return res
def countPermutations(ar, n):
mp = dict()
ans = 1
cnt = n
for i in range(n):
if (ar[i] in mp):
mp[ar[i]] += 1
else:
mp[ar[i]] = 1
for i in range(n):
if (i not in mp):
break
ans = (ans * mp[i])
cnt -= 1
ans = ans * factorial(cnt)
return ans
arr = [1, 0, 1]
N = len(arr)
print(countPermutations(arr, N))
|
C#
using System;
using System.Collections.Generic;
public class GFG
{
static int factorial(int n)
{
int res = 1, i;
for (i = 2; i <= n; i++) {
res *= i;
}
return res;
}
static int countPermutations(int[] ar, int n)
{
Dictionary<int, int> mp = new Dictionary<int, int>();
int ans = 1, cnt = n, i;
for (i = 0; i < n; i++) {
if (mp.ContainsKey(ar[i]))
{
mp[ar[i]] = mp[ar[i]] + 1;
}
else
{
mp.Add(ar[i], 1);
}
}
for (i = 0; i < n; i++) {
if (! mp.ContainsKey(i)) {
break;
}
ans = (ans * mp[i]);
cnt--;
}
ans = ans * factorial(cnt);
return ans;
}
public static void Main(String[] args)
{
int[] arr = { 1, 0, 1 };
int N = arr.Length;
Console.Write(countPermutations(arr, N));
}
}
|
Javascript
<script>
function factorial(n) {
let res = 1, i;
for (i = 2; i <= n; i++) {
res *= i;
}
return res;
}
function countPermutations(ar, n) {
let mp = new Map();
let ans = 1, cnt = n;
for (let i = 0; i < n; i++) {
if (mp.has(ar[i])) {
mp.set(ar[i], mp.get(ar[i]) + 1)
}
else {
mp.set(ar[i], 1)
}
}
for (let i = 0; i < n; i++) {
if (!mp.has(i)) {
break;
}
ans = (ans * mp.get(i));
cnt--;
}
ans = ans * factorial(cnt);
return ans;
}
let arr = [1, 0, 1];
let N = arr.length
document.write(countPermutations(arr, N));
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...