Count of pairs of integers whose difference of squares is equal to N
Last Updated :
15 Nov, 2022
Given a positive integer N, the task is to find the count of pairs of integers (x, y) whose difference of squares is equal to N, i.e.,
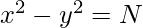
Examples:
Input: N = 20
Output: 4
Explanation:
The 4 possible pairs are (10, 2), (-10, 2), (-10, -2) and (10, -2).
Input: N = 80
Output: 12
Explanation:
The 12 possible pairs are:
1. (40, 2), (-40, 2), (-40, -2) and (40, -2).
2. (20, 4), (-20, 4), (-20, -4) and (20, -4).
3. (10, 8), (-10, 8), (-10, -8) and (10, -8).
Approach:
The given equation can also be written as:
=> 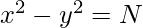
=> 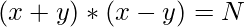
Now for an integral solution of the given equation:
(x+y)(x-y)
is always an integer
=> (x+y)(x-y)
are divisors of N
Let (x + y) = p1 and (x + y) = p2
be the two equations where p1 & p2 are the divisors of N
such that p1 * p2 = N.
Solving for the above two equations we have:
=> 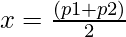
and 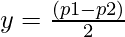
From the above calculations, for x and y to be integral, then the sum of divisors must be even. Since there are 4 possible values for two values of x and y as (+x, +y), (+x, -y), (-x, +y) and (-x, -y).
Therefore the total number of possible solutions is given by 4*(count pairs of divisors with even sum).
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void findSolutions(int N)
{
int count = 0;
for (int i = 1; i <= sqrt(N); i++) {
if (N % i == 0) {
if ((i + N / i) % 2 == 0) {
count++;
}
}
}
cout << 4 * count << endl;
}
int main()
{
int N = 80;
findSolutions(N);
return 0;
}
|
Java
import java.util.*;
class GFG{
static void findSolutions(int N)
{
int count = 0;
for(int i = 1; i <= Math.sqrt(N); i++)
{
if (N % i == 0)
{
if ((i + N / i) % 2 == 0)
{
count++;
}
}
}
System.out.print(4 * count);
}
public static void main(String[] args)
{
int N = 80;
findSolutions(N);
}
}
|
Python3
import math;
def findSolutions(N):
count = 0;
for i in range(1, int(math.sqrt(N)) + 1):
if (N % i == 0):
if ((i + N // i) % 2 == 0):
count += 1;
print(4 * count);
N = 80;
findSolutions(N);
|
C#
using System;
class GFG{
static void findSolutions(int N)
{
int count = 0;
for(int i = 1; i <= Math.Sqrt(N); i++)
{
if (N % i == 0)
{
if ((i + N / i) % 2 == 0)
{
count++;
}
}
}
Console.Write(4 * count);
}
public static void Main(String[] args)
{
int N = 80;
findSolutions(N);
}
}
|
Javascript
<script>
function findSolutions(N)
{
let count = 0;
for(let i = 1; i <= Math.sqrt(N); i++)
{
if (N % i == 0)
{
if ((i + parseInt(N / i)) % 2 == 0)
{
count++;
}
}
}
document.write(4 * count + "<br>");
}
let N = 80;
findSolutions(N);
</script>
|
Output:
12
Time Complexity: O(sqrt(N))
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...