Count of pairs from Array with sum equal to twice their bitwise AND
Last Updated :
18 Aug, 2022
Given an array arr[], the task is to count the pairs in the array with sum equal to twice their bitwise AND, i.e., 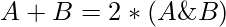
Examples:
Input: arr[] = {1, 1, 3, 4, 4, 5, 7, 8}
Output: 2
Explanation:
Pairs with sum equal to twice their bitwise AND:
{(1, 1), (4, 4)}
Input: arr[] = {1, 3, 3, 5, 4, 6}
Output: 1
Naive Approach: A simple solution is to iterate over every possible pair and check that if the sum of the pair is equal to the twice the Bit-wise AND of the pair. If the pair have the equal sum and bitwise AND then increment the count of such pairs by 1.
Efficient Approach: The idea is to use the relation between the sum and the bitwise AND. That is –
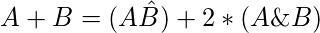
In this for equal sum and the bitwise AND, the value of the Bitwise XOR of the pair should be equal to 0. We know that the Bitwise XOR of any two pairs is equal to 0 only if they are equal to each other. Therefore, if X is the frequency of the element. Then increment the count of pairs by 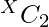 .
.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
map<int, int> mp;
int find_pairs(int ar[], int n)
{
int ans = 0;
for (int i = 0; i < n; i++) {
mp[ar[i]]++;
}
for (auto i : mp) {
int count = i.second;
if (count > 1) {
ans += ((count
* (count - 1))
/ 2);
}
}
return ans;
}
int main()
{
int ar[]
= { 1, 2, 3, 3, 4,
5, 5, 7, 8 };
int arr_size = (sizeof(ar)
/ sizeof(ar[0]));
cout << find_pairs(ar, arr_size);
return 0;
}
|
Java
import java.util.*;
class GFG{
static HashMap<Integer,
Integer> mp = new HashMap<Integer,
Integer>();
static int find_pairs(int arr[], int n)
{
int ans = 0;
for(int i = 0; i < n; i++)
{
if(mp.containsKey(arr[i]))
{
mp.put(arr[i], mp.get(arr[i]) + 1);
}
else
{
mp.put(arr[i], 1);
}
}
for(Map.Entry<Integer, Integer> i:mp.entrySet())
{
int count = i.getValue();
if (count > 1)
{
ans += ((count * (count - 1)) / 2);
}
}
return ans;
}
public static void main(String[] args)
{
int arr[] = { 1, 2, 3, 3, 4,
5, 5, 7, 8 };
int arr_size = arr.length;
System.out.print(find_pairs(arr, arr_size));
}
}
|
Python3
from collections import defaultdict
mp = defaultdict(int)
def find_pairs(arr, n):
ans = 0
for i in range(n):
mp[arr[i]] += 1
for i in mp.values():
count = i
if (count > 1):
ans += ((count * (count - 1)) // 2)
return ans
if __name__ == "__main__":
arr = [ 1, 2, 3, 3, 4,
5, 5, 7, 8 ]
arr_size = len(arr)
print(find_pairs(arr, arr_size))
|
C#
using System;
using System.Collections.Generic;
class GFG{
static Dictionary<int,
int> mp = new Dictionary<int,
int>();
static int find_pairs(int []arr, int n)
{
int ans = 0;
for(int i = 0; i < n; i++)
{
if(mp.ContainsKey(arr[i]))
{
mp[arr[i]] = mp[arr[i]] + 1;
}
else
{
mp.Add(arr[i], 1);
}
}
foreach(KeyValuePair<int, int> i in mp)
{
int count = i.Value;
if (count > 1)
{
ans += ((count * (count - 1)) / 2);
}
}
return ans;
}
public static void Main(String[] args)
{
int []arr = { 1, 2, 3, 3, 4,
5, 5, 7, 8 };
int arr_size = arr.Length;
Console.Write(find_pairs(arr, arr_size));
}
}
|
Javascript
<script>
let mp = new Map();
function find_pairs(arr,n)
{
let ans = 0;
for(let i = 0; i < n; i++)
{
if(mp.has(arr[i]))
{
mp.set(arr[i], mp.get(arr[i]) + 1);
}
else
{
mp.set(arr[i], 1);
}
}
for(let [key, value] of mp.entries())
{
let count = value;
if (count > 1)
{
ans += ((count * (count - 1)) / 2);
}
}
return ans;
}
let arr=[1, 2, 3, 3, 4,
5, 5, 7, 8];
let arr_size = arr.length;
document.write(find_pairs(arr, arr_size));
</script>
|
Time complexity: O(nlogn) where n is number of elements in the given array
Auxiliary Space: O(n)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...