Count of pairs (arr[i], arr[j]) such that arr[i] + j and arr[j] + i are equal

Given an array arr[], the task is to count pairs i, j such that, i < j and arr[i] + j = arr[j] + i.

Examples:

Input: arr[] = {4, 1, 2, 3}
Output: 3
Explanation: In total three pairs are satisfying the given condition those are {1, 2}, {2, 3} and {1, 3}.
So, the final answer is 3. 

Input: arr[] = {1, 5, 6}
Output: 1

Naive Approach: The naive approach for solving this problem is to check for each and every pair of the array for the given condition and count those pairs.

Time Complexity: O(N²), Where N is the size of arr[]. 

In order to get every pair we need to run two nested loops. Thus the time complexity will be O(N²).

Auxiliary Space: O(1).

As constant extra space is used.

Efficient approach: This problem can be solved by using hashmaps. At first, we can twist the condition that is given to us we can change arr[j] + i= arr[i]+ j it to arr[j] – j = arr[i] – i, which means two different numbers having the same difference in their value and index. That makes it easy, Now follow the steps below to solve the given problem. 

• Create a map mp and a variable say, ans = 0, to store the answer.
• Traverse the whole array arr[] with say i.
  • For each element, we will find out the difference in its value and index, simply a[i] – i.
  • If there is some value present in the map that means there are other numbers with the same value so we will add those frequencies to the answer.
  • Increase the value of mp[a[i] – i].
• Return ans as the final answer.

Below is the implementation of the above approach:

C++

#include <bits/stdc++.h>
using namespace std;

// Function to count pairs with given properties
int solve(int N, int arr[])
{
    // Map for the storing the frequency
    // of a given difference
    map<int, int> mp;

    // Variable to store the final ans
    int ans = 0;

    // Traverse the array and update mp
    for (int i = 0; i < N; i++) {
        ans += mp[arr[i] - i];
        mp[arr[i] - i]++;
    }

    // Return the final result
    return ans;
}

int main()
{
    int N = 4;
    int arr[] = { 4, 1, 2, 3 };

    // Print the result
    cout << solve(N, arr);
    return 0;
}

Java

import java.util.*;

class GFG{

// Function to count pairs with given properties
static int solve(int N, int arr[])
{

    // Map for the storing the frequency
    // of a given difference
    HashMap<Integer,Integer> mp = new HashMap<Integer,Integer>();

    // Variable to store the final ans
    int ans = 0;

    // Traverse the array and update mp
    for (int i = 0; i < N; i++) {
        if(mp.containsKey(arr[i]-i)){
            ans+=mp.get(arr[i]-i);
            mp.put(arr[i]-i, mp.get(arr[i]-i)+1);
        }
        else{
            mp.put(arr[i]-i, 1);
        }
    }

    // Return the final result
    return ans;
}

public static void main(String[] args)
{
    int N = 4;
    int arr[] = { 4, 1, 2, 3 };

    // Print the result
    System.out.print(solve(N, arr));
}
}

// This code is contributed by shikhasingrajput

Python3

# Python Program to implement
# the above approach

# Function to count pairs with given properties
def solve(N, arr):

    # Map for the storing the frequency
    # of a given difference
    mp = dict()

    # Variable to store the final ans
    ans = 0

    # Traverse the array and update mp
    for i in range(N):

        if ((arr[i] - i) not in mp):
            mp[arr[i] - i] = 0

        ans += mp[arr[i] - i]
        mp[arr[i] - i] = mp[arr[i] - i] + 1

    # Return the final result
    return ans

N = 4
arr = [4, 1, 2, 3]

# Print the result
print(solve(N, arr))

# This code is contributed by Saurabh Jaiswal

C#

using System;
using System.Collections.Generic;

public class GFG{

// Function to count pairs with given properties
static int solve(int N, int []arr)
{

    // Map for the storing the frequency
    // of a given difference
    Dictionary<int,int> mp = new Dictionary<int,int>();

    // Variable to store the readonly ans
    int ans = 0;

    // Traverse the array and update mp
    for (int i = 0; i < N; i++) {
        if(mp.ContainsKey(arr[i]-i)){
            ans+=mp[arr[i]-i];
            mp[arr[i]-i]= mp[arr[i]-i]+1;
        }
        else{
            mp.Add(arr[i]-i, 1);
        }
    }

    // Return the readonly result
    return ans;
}

public static void Main(String[] args)
{
    int N = 4;
    int []arr = { 4, 1, 2, 3 };

    // Print the result
    Console.Write(solve(N, arr));
}
}

// This code is contributed by 29AjayKumar

Javascript

<script>
        // JavaScript Program to implement
        // the above approach

        // Function to count pairs with given properties
        function solve(N, arr)
        {

            // Map for the storing the frequency
            // of a given difference
            let mp = new Map();

            // Variable to store the final ans
            let ans = 0;

            // Traverse the array and update mp
            for (let i = 0; i < N; i++) {

                if (mp.has(arr[i] - i) == false) {
                    mp.set(arr[i] - i, 0)
                }
                ans += mp.get(arr[i] - i);
                mp.set(arr[i] - i, mp.get(arr[i] - i) + 1);
            }

            // Return the final result
            return ans;
        }

        let N = 4;
        let arr = [4, 1, 2, 3];

        // Print the result
        document.write(solve(N, arr));

    // This code is contributed by Potta Lokesh
    </script>

Output

3

Time Complexity: 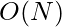, where N is the size of the array.

Auxiliary Space: O(N), where N is the size of the array.