Count of nested polygons that can be drawn by joining vertices internally

Given a regular polygon with N sides. The task is to find the count of polygons that can be drawn from the given polygon by joining the vertices of the given polygon internally.

Examples:

Input: N = 6
Output: 1
Explanation:

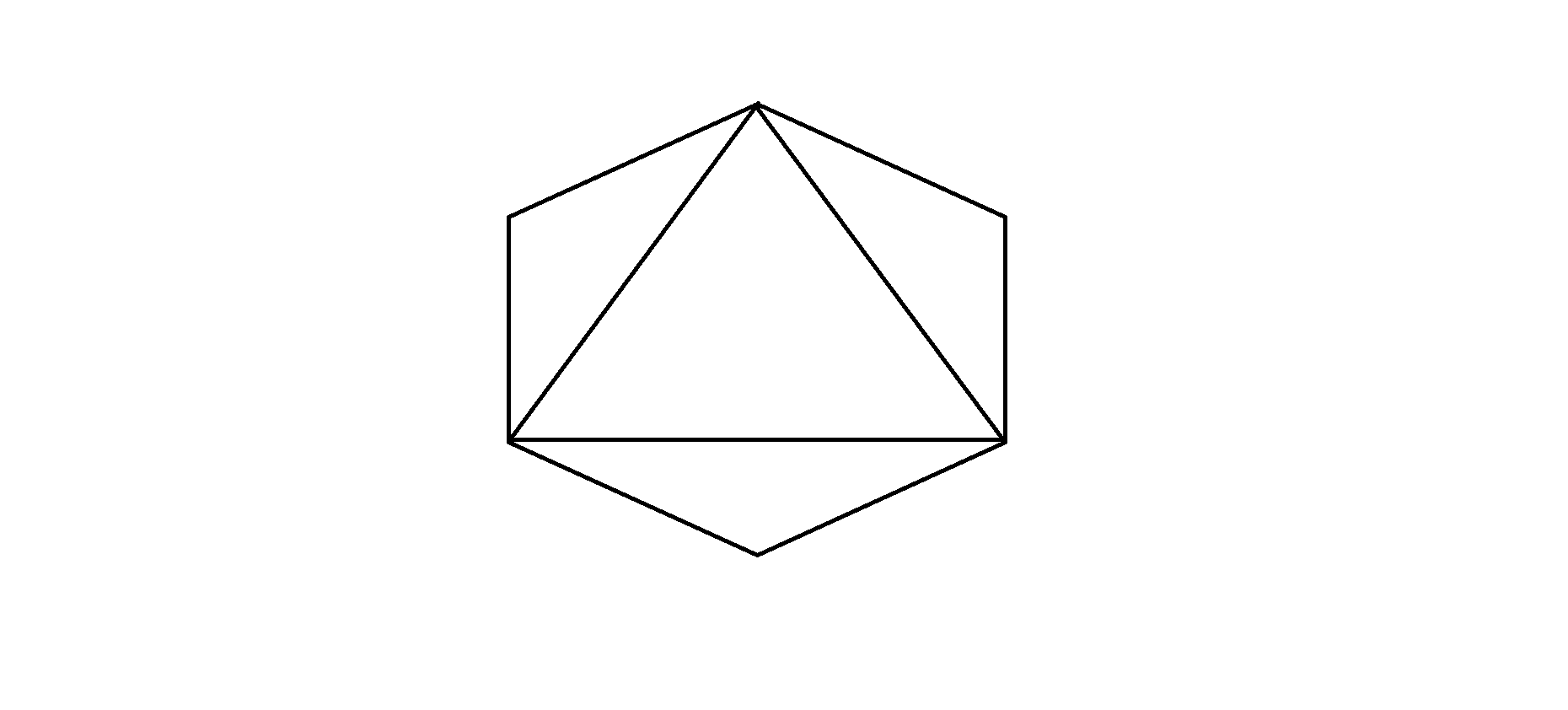
There is only one nested polygon i.e., Triangle whose sides are the chords of the immediate parent polygon i.e., Hexagon.

Input: N = 12
Output: 2
Explanation: 

There are two nested polygons. First one is a Hexagon and second one is a Triangle. The sides of both of the nested polygons are actually chords of their immediate parent polygon.

Approach: To solve this problem observe the following:

1. Polygons with a number of sides less than or equal to 5 can not produce nested polygons, i.e. polygons of sides ?5 will always have at least one side overlapping with its nested polygon.
2. Each side of a nested polygon takes two consecutive sides of the immediate parent polygon.

With the above observations, it is easy to conclude that number of sides of each nested polygon is half of the number of sides of its immediate parent polygon. So, we keep dividing N by 2, and increment the counter for nested polygons, until N becomes less than or equal to 5.

Below is the implementation of the above approach:

C++

// C++ program for the above approach

#include <iostream>
using namespace std;

// Function that counts the nested
// polygons inside another polygons
int countNestedPolygons(int sides)
{
    // Stores the count
    int count = 0;

    // Child polygons can only existss
    // if parent polygon has sides > 5
    while (sides > 5) {

        // Get next nested polygon
        sides /= 2;
        count += 1;
    }

    // Return the count
    return count;
}

// Driver Code
int main()
{
    // Given side of polygon
    int N = 12;

    // Function Call
    cout << countNestedPolygons(N);

    return 0;
}

Java

// Java program for the above approach
class GFG{

// Function that counts the nested
// polygons inside another polygons
static int countNestedPolygons(int sides)
{
    // Stores the count
    int count = 0;

    // Child polygons can only existss
    // if parent polygon has sides > 5
    while (sides > 5)
    {

        // Get next nested polygon
        sides /= 2;
        count += 1;
    }

    // Return the count
    return count;
}

// Driver Code
public static void main(String[] args)
{
    // Given side of polygon
    int N = 12;

    // Function Call
    System.out.print(countNestedPolygons(N));
}
}

// This code is contributed by Rajput-Ji

Python3

# Python3 program for the above approach

# Function that counts the nested
# polygons inside another polygons
def countNestedPolygons(sides):

    # Stores the count
    count = 0

    # Child polygons can only exists
    # if parent polygon has sides > 5
    while (sides > 5):

        # Get next nested polygon
        sides //= 2
        count += 1

    # Return the count
    return count

# Driver Code

# Given side of polygon
N = 12

# Function call
print(countNestedPolygons(N))

# This code is contributed by vishu2908

C#

// C# program for the above approach
using System;

class GFG{

// Function that counts the nested
// polygons inside another polygons
static int countNestedPolygons(int sides)
{

    // Stores the count
    int count = 0;

    // Child polygons can only existss
    // if parent polygon has sides > 5
    while (sides > 5)
    {

        // Get next nested polygon
        sides /= 2;
        count += 1;
    }

    // Return the count
    return count;
}

// Driver Code
public static void Main(String[] args)
{

    // Given side of polygon
    int N = 12;

    // Function call
    Console.Write(countNestedPolygons(N));
}
}

// This code is contributed by Rajput-Ji

Javascript

<script>

// JavaScript program for the above approach
// Function that counts the nested
// polygons inside another polygons
function countNestedPolygons(sides)
{
    // Stores the count
    var count = 0;

    // Child polygons can only existss
    // if parent polygon has sides > 5
    while (sides > 5)
    {

        // Get next nested polygon
        sides /= 2;
        count += 1;
    }

    // Return the count
    return count;
}

// Driver Code
// Given side of polygon
var N = 12;

// Function Call
document.write(countNestedPolygons(N));

// This code contributed by shikhasingrajput

</script>

Output:

2

Time Complexity: O(log N), where N is the number of vertices in the given polygon.
Auxiliary Space: O(1)