Count of N-bit odd and even integers with K set bits
Last Updated :
26 Aug, 2021
Given two positive integers N and K, the task is to count the number of even and odd integers consisting of N bits, out of which K bits are set.
Examples:
Input: N = 5, K = 2
Output: 3 1
Explanation:
The 5 bit even integers having 2 set bits are: 10010(= 18), 10100(= 20), 11000(= 24). So, the count is 3.
The 5 bit odd integer having 2 set bits is 10001(=17). So, the count is 1.
Input: N = 5, K = 5
Output: 0 1
Approach: The given problem can be solved using the following observations:
- For any N bit integer, the Nth bit(most significant bit) must be a set bit.
- For any N bit integer to be odd, the 1st bit (least significant bit) must be a set bit.
- For any N bit integer to be even, the 1st bit (least significant bit) must not be a set bit.
Therefore, the number of even integers can be obtained by fixing the Nth bit as 1 and the 1st bit as 0 and calculating the number of ways to arrange the remaining bits. Similarly, the number of odd integers can be obtained by fixing the 1st and the Nth bit as 1.
The total number of distinct ways to arrange X bits having Y set bits is given by:
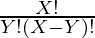
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
long long factorial(int n)
{
long long ans = 1;
while (n >= 1) {
ans *= n;
n--;
}
return ans;
}
void Binary_Num(int n, int k)
{
long long num_even, num_odd;
if (n - k - 1 >= 0 && k - 1 >= 0) {
num_even
= factorial(n - 2)
/ (factorial(k - 1) * factorial(n - k - 1));
}
else {
num_even = 0;
}
if (k - 2 >= 0) {
num_odd = factorial(n - 2)
/ (factorial(k - 2) * factorial(n - k));
}
else {
num_odd = 0;
}
cout << num_even << " " << num_odd << endl;
}
int main()
{
int N = 9, K = 6;
Binary_Num(N, K);
return 0;
}
|
Java
import java.io.*;
class GFG {
static long factorial(int n)
{
long ans = 1;
while (n >= 1) {
ans *= n;
n--;
}
return ans;
}
static void Binary_Num(int n, int k)
{
long num_even, num_odd;
if (n - k - 1 >= 0 && k - 1 >= 0) {
num_even
= factorial(n - 2)
/ (factorial(k - 1) * factorial(n - k - 1));
}
else {
num_even = 0;
}
if (k - 2 >= 0) {
num_odd = factorial(n - 2)
/ (factorial(k - 2) * factorial(n - k));
}
else {
num_odd = 0;
}
System.out.println( num_even +" " +num_odd );
}
public static void main(String[] args)
{
int N = 9, K = 6;
Binary_Num(N, K);
}
}
|
Python3
import math
def Binary_Num(N, K):
if N-K-1 >= 0 and K-1 >= 0:
num_even = math.factorial(
N-2)/(math.factorial(K-1)
* math.factorial(N-K-1))
else:
num_even = 0
if K-2 >= 0:
num_odd = math.factorial(N-2) \
/ (math.factorial(K-2)
* math.factorial(N-K))
else:
num_odd = 0
print(int(num_even), int(num_odd))
if __name__ == "__main__":
N = 9
K = 6
Binary_Num(N, K)
|
C#
using System;
using System.Collections.Generic;
class GFG{
static int factorial(int n)
{
int ans = 1;
while (n >= 1) {
ans *= n;
n--;
}
return ans;
}
static void Binary_Num(int n, int k)
{
int num_even, num_odd;
if (n - k - 1 >= 0 && k - 1 >= 0) {
num_even
= factorial(n - 2)
/ (factorial(k - 1) * factorial(n - k - 1));
}
else {
num_even = 0;
}
if (k - 2 >= 0) {
num_odd = factorial(n - 2)
/ (factorial(k - 2) * factorial(n - k));
}
else {
num_odd = 0;
}
Console.Write(num_even + " " + num_odd);
}
public static void Main()
{
int N = 9, K = 6;
Binary_Num(N, K);
}
}
|
Javascript
<script>
function factorial(n) {
let ans = 1;
while (n >= 1) {
ans *= n;
n--;
}
return ans;
}
function Binary_Num(n, k) {
let num_even, num_odd;
if (n - k - 1 >= 0 && k - 1 >= 0) {
num_even
= Math.floor(factorial(n - 2)
/ (factorial(k - 1) * factorial(n - k - 1)));
}
else {
num_even = 0;
}
if (k - 2 >= 0) {
num_odd = Math.floor(factorial(n - 2)
/ (factorial(k - 2) * factorial(n - k)));
}
else {
num_odd = 0;
}
document.write(num_even + " " + num_odd + "<br>");
}
let N = 9, K = 6;
Binary_Num(N, K);
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(1)
Note: For multiple queries, precompute the factorial values in an array which will result in O(1) time per query and O(N) for precomputation.
Share your thoughts in the comments
Please Login to comment...