Count of elements that are binary searchable in the given array

Given an array arr[] consisting of N integers, the task is to find the maximum count of integers that are binary searchable in the given array.

Examples:

Input: arr[] = {1, 3, 2}
Output: 2
Explanation: arr[0], arr[1] can be found.

Input: arr[] = {3, 2, 1, 10, 23, 22, 21}
Output: 3
Explanation: arr[1], arr[3], arr[5] can be found using binary search irrespective of whether the array is sorted or not.

Approach: The given problem can be solved by searching for each element separately in the array using the Binary Search approach and increment the count of those integers that exist in the array. Follow the below steps to solve the problem:

• Make a variable count = 0, that will store the count of elements that are binary searchable.
• For each element perform the binary search in the range [0, N) as:
  • Initialize the variable l as 0 and r as N-1 and perform the binary search for arr[i].
  • For each iteration of the while loop till l is less than equal to r, calculate the mid-value denoted by (l + r)/2.
    • If arr[mid] equals arr[i] then increment count by 1.
    • If arr[mid] is less than arr[i], then change l as mid + 1.
    • Otherwise, change r as mid – 1.
• The final answer will be stored in the variable count.

Below is the implementation of the above approach:

C++

// C++ program for the above approach

#include <bits/stdc++.h>
using namespace std;

// Function to find the total count of
// elements that are binary searchable
int totalBinarySearchable(vector<int> arr)
{

    // Stores the count of element that
    // are binary searchable
    int count = 0;
    int N = arr.size();

    // For each element check if it can
    // be found by doing a binary search
    for (int i = 0; i < N; i++) {

        // Binary search range
        int l = 0, r = N - 1;

        // Do a binary Search
        while (l <= r) {
            int mid = (l + r) / 2;

            // Array element found
            if (arr[mid] == arr[i]) {
                count++;
                break;
            }
            if (arr[mid] < arr[i]) {
                l = mid + 1;
            }
            else {
                r = mid - 1;
            }
        }
    }

    // Return the total count
    return count;
}

// Driver Code
int main()
{
    vector<int> arr = { 3, 2, 1, 10, 23, 22, 21 };
    cout << totalBinarySearchable(arr);

    return 0;
}

Java

// Java code for the above approach
import java.io.*;

class GFG {

    // Function to find the total count of
    // elements that are binary searchable
    static int totalBinarySearchable(int[] arr)
    {

        // Stores the count of element that
        // are binary searchable
        int count = 0;
        int N = arr.length;

        // For each element check if it can
        // be found by doing a binary search
        for (int i = 0; i < N; i++) {

            // Binary search range
            int l = 0, r = N - 1;

            // Do a binary Search
            while (l <= r) {
                int mid = (l + r) / 2;

                // Array element found
                if (arr[mid] == arr[i]) {
                    count++;
                    break;
                }
                if (arr[mid] < arr[i]) {
                    l = mid + 1;
                }
                else {
                    r = mid - 1;
                }
            }
        }

        // Return the total count
        return count;
    }

    // Driver Code
    public static void main(String[] args)
    {
        int[] arr = { 3, 2, 1, 10, 23, 22, 21 };

        System.out.println(totalBinarySearchable(arr));
    }
}

// This code is contributed by Potta Lokesh

Python3

# python program for the above approach

# Function to find the total count of
# elements that are binary searchable


def totalBinarySearchable(arr):

        # Stores the count of element that
        # are binary searchable
    count = 0
    N = len(arr)

    # For each element check if it can
    # be found by doing a binary search
    for i in range(0, N):

                # Binary search range
        l = 0
        r = N - 1

        # Do a binary Search
        while (l <= r):
            mid = (l + r) // 2

            # Array element found
            if (arr[mid] == arr[i]):
                count += 1
                break

            if (arr[mid] < arr[i]):
                l = mid + 1

            else:
                r = mid - 1

        # Return the total count
    return count


# Driver Code
if __name__ == "__main__":

    arr = [3, 2, 1, 10,
           23, 22, 21]
    print(totalBinarySearchable(arr))

    # This code is contributed by rakeshsahni

C#

// C# code for the above approach
using System;
public class GFG {

    // Function to find the total count of
    // elements that are binary searchable
    static int totalBinarySearchable(int[] arr)
    {

        // Stores the count of element that
        // are binary searchable
        int count = 0;
        int N = arr.Length;

        // For each element check if it can
        // be found by doing a binary search
        for (int i = 0; i < N; i++) {

            // Binary search range
            int l = 0, r = N - 1;

            // Do a binary Search
            while (l <= r) {
                int mid = (l + r) / 2;

                // Array element found
                if (arr[mid] == arr[i]) {
                    count++;
                    break;
                }
                if (arr[mid] < arr[i]) {
                    l = mid + 1;
                }
                else {
                    r = mid - 1;
                }
            }
        }

        // Return the total count
        return count;
    }

    // Driver Code
    public static void Main(string[] args)
    {
        int[] arr = { 3, 2, 1, 10, 23, 22, 21 };

        Console.WriteLine(totalBinarySearchable(arr));
    }
}

// This code is contributed by rrrtnx.

Javascript

<script>
// Javascript program for the above approach

// Function to find the total count of
// elements that are binary searchable
function totalBinarySearchable(arr)
{

  // Stores the count of element that
  // are binary searchable
  let count = 0;
  let N = arr.length;

  // For each element check if it can
  // be found by doing a binary search
  for (let i = 0; i < N; i++)
  {

    // Binary search range
    let l = 0,
      r = N - 1;

    // Do a binary Search
    while (l <= r) {
      let mid = Math.floor((l + r) / 2);

      // Array element found
      if (arr[mid] == arr[i]) {
        count++;
        break;
      }
      if (arr[mid] < arr[i]) {
        l = mid + 1;
      } else {
        r = mid - 1;
      }
    }
  }

  // Return the total count
  return count;
}

// Driver Code
let arr = [3, 2, 1, 10, 23, 22, 21];
document.write(totalBinarySearchable(arr));

// This code is contributed by gfgking.
</script>

Output

3

Time Complexity: O(N*log(N))
Auxiliary Space: O(1)

Approach 2: This problem can also be solved in linear time complexity.

In the previous approach, we were checking if for all a[i] belonging to array a, it was binary searchable or not. The problem with this approach is that we were visiting some of the elements multiple times to check ordering conditions. Rather than doing, this while we are visiting a node, we can mark it as binary searchable or not binary searchable. When constructing a binary tree for the array, it should be noted that the traversal is towards the right, when the target element is greater than the root or towards the left, when the target element is smaller than the root element. Now, given a path, the target element should be greater than the maximum of all root nodes via which the path of searching deviated towards the right, and smaller than the minimum of all values via which the path deviated towards the left.

To better understand this, create a tree representation of the process of binary search on the array. For eg:

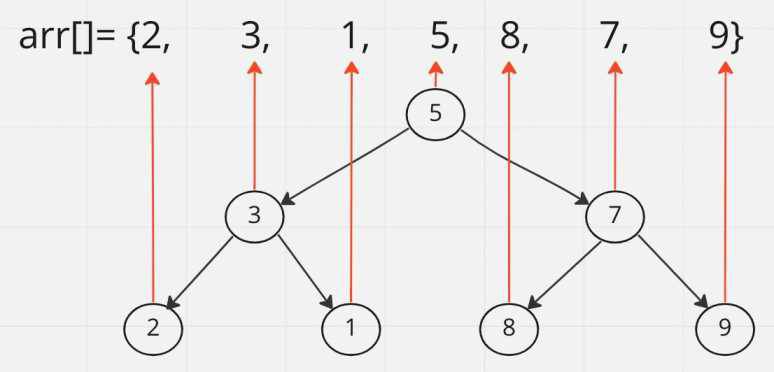
Conversion of the given array to Binary Search Tree

In the binary search technique, the root node is actually the middle element of all the elements in that subtree. For eg:
Node 5 is the middle element of array [2, 3, 1, 5, 8, 7, 9]
and Node 3 is the middle element of array [2, 3, 1]

Example:

Now, Let’s search for node 1 in the above array. So, target = 1

Initially, In Binary Search: left = 0, right = 6.

arr[] = {2, 3, 1,  5, 8, 7, 9}

First Iteration: middle = (left + right) / 2 = 3 (arr[3] = 5)

Comparing middle element with target.

Since 5 > 1, so, right = middle – 1 = 3 – 1 = 2.

arr[] = {2, 3, 1}

Second Iteration: middle = (0 + 2) / 2 = 1 (arr[1] = 3)

Comparing middle element with target.

Since 3 > 1, so right = middle – 1 = 1 – 1 = 0.

arr[] = {2}

Comparing middle element with target. The values don’t match.(arr[0]!=1)

Hence, 1 is not binary searchable.

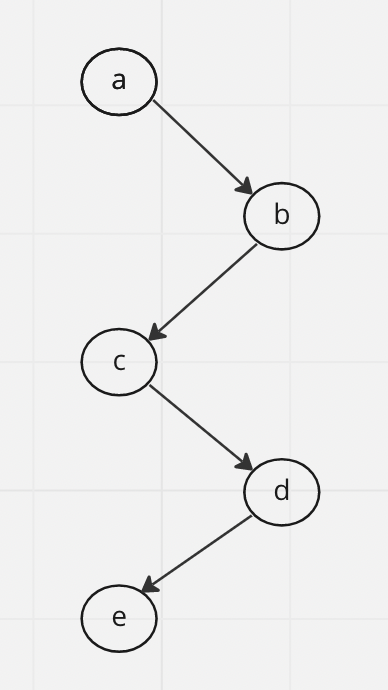
The path needs to be traversed for node e to be binary searchable

In the above Figure, for node e to be binary searchable:

If we want to search e, then e must be greater than a and c because of BST (binary search tree) conventions. also, e must be smaller than b and d. If this is not the case, then e is not binary searchable.

So, we can summarise the condition as; 
1. e < min(b, d)
2. e > max(a, c)

Below is the implementation of the above approach:

C++

#include <bits/stdc++.h>
using namespace std;

int countBinarySearchableIndex(int Arr[], int l, int r,
                               int LR, int RL)
{
    // Invalid indexes
    if (l > r)
        return 0;
    int ans = 0;

    // Finding the middle element of the current array
    // (arr[l], ... arr[r]) Similar to as we do in binary
    // search
    int m = (l + r) / 2;

    // If these conditions follow that means Arr[m] is
    // binary searchable.
    if (LR < Arr[m] && Arr[m] < RL)
        ans = 1;

    // Finding the binary searchable elements to the left of
    // middle(m) element
    int l_ans = countBinarySearchableIndex(
        Arr, l, m - 1, LR, min(RL, Arr[m]));

    // Finding the binary searchable elements to the right
    // of middle(m) element
    int r_ans = countBinarySearchableIndex(
        Arr, m + 1, r, max(LR, Arr[m]), RL);

    return ans + l_ans + r_ans;
}

int main()
{
    int Arr[] = { 10, 1,  2, 3, 4,  8,  6, 5,
                  7,  12, 9, 8, 13, 15, 11 };
    int n = 15;
    cout << "Number of Binary Searchable Indexes: ";
    cout << countBinarySearchableIndex(Arr, 0, n - 1, -1e9,
                                       1e9)
         << endl;
    return 0;
}

Java

// Java code addition for the above approach

import java.io.*;

class GFG {

    static int countBinarySearchableIndex(int[] Arr, int l,
                                          int r, int LR,
                                          int RL)
    {
        // Invalid indexes
        if (l > r)
            return 0;
        int ans = 0;

        // Finding the middle element of the current array
        // (arr[l], ... arr[r]) Similar to as we do in
        // binary search
        int m = (l + r) / 2;

        // If these conditions follow that means Arr[m] is
        // binary searchable.
        if (LR < Arr[m] && Arr[m] < RL)
            ans = 1;

        // Finding the binary searchable elements to the
        // left of middle(m) element
        int l_ans = countBinarySearchableIndex(
            Arr, l, m - 1, LR, Math.min(RL, Arr[m]));

        // Finding the binary searchable elements to the
        // right of middle(m) element
        int r_ans = countBinarySearchableIndex(
            Arr, m + 1, r, Math.max(LR, Arr[m]), RL);

        return ans + l_ans + r_ans;
    }

    public static void main(String[] args)
    {
        int[] Arr = { 10, 1,  2, 3, 4,  8,  6, 5,
                      7,  12, 9, 8, 13, 15, 11 };

        int n = 15;
        System.out.print(
            "Number of Binary Searchable Indexes: ");
        System.out.println(countBinarySearchableIndex(
            Arr, 0, n - 1, (int)-1e9, (int)1e9));
    }
}

// This code is contributed by lokesh

Python3

# Python code addition for the above approach
def countBinarySearchableIndex(Arr, l, r, LR, RL):
    # Invalid indexes
    if l > r:
        return 0
    ans = 0

    # Finding the middle element of the current array
    # (arr[l], ... arr[r]) Similar to as we do in
    # binary search
    m = (l + r) // 2

    # If these conditions follow that means Arr[m] is
    # binary searchable.
    if LR < Arr[m] and Arr[m] < RL:
        ans = 1

    # Finding the binary searchable elements to the
    # left of middle(m) element
    l_ans = countBinarySearchableIndex(
        Arr, l, m - 1, LR, min(RL, Arr[m]))

    # Finding the binary searchable elements to the
    # right of middle(m) element
    r_ans = countBinarySearchableIndex(
        Arr, m + 1, r, max(LR, Arr[m]), RL)

    return ans + l_ans + r_ans


Arr = [10, 1, 2, 3, 4, 8, 6, 5, 7, 12, 9, 8, 13, 15, 11]
n = 15
print("Number of Binary Searchable Indexes: ", end="")
print(countBinarySearchableIndex(Arr, 0, n - 1, -1e9, 1e9))

# This code is contributed by lokeshmvs21.

C#

// C# code addition for the above approach
using System;
public class GFG {

  static int countBinarySearchableIndex(int[] Arr, int l,
                                        int r, int LR,
                                        int RL)
  {
    // Invalid indexes
    if (l > r)
      return 0;
    int ans = 0;

    // Finding the middle element of the current array
    // (arr[l], ... arr[r]) Similar to as we do in
    // binary search
    int m = (l + r) / 2;

    // If these conditions follow that means Arr[m] is
    // binary searchable.
    if (LR < Arr[m] && Arr[m] < RL)
      ans = 1;

    // Finding the binary searchable elements to the
    // left of middle(m) element
    int l_ans = countBinarySearchableIndex(
      Arr, l, m - 1, LR, Math.Min(RL, Arr[m]));

    // Finding the binary searchable elements to the
    // right of middle(m) element
    int r_ans = countBinarySearchableIndex(
      Arr, m + 1, r, Math.Max(LR, Arr[m]), RL);

    return ans + l_ans + r_ans;
  }

  static public void Main()
  {

    // Code
    int[] Arr = { 10, 1,  2, 3, 4,  8,  6, 5,
                 7,  12, 9, 8, 13, 15, 11 };

    int n = 15;
    Console.Write(
      "Number of Binary Searchable Indexes: ");
    Console.WriteLine(countBinarySearchableIndex(
      Arr, 0, n - 1, (int)-1e9, (int)1e9));
  }
}

// This code is contributed by lokesh

Javascript

// Javascript code for the above approach
function countBinarySearchableIndex(Arr, l, r, LR, RL)
{
    // Invalid indexes
    if (l > r)
        return 0;
    let ans = 0;

    // Finding the middle element of the current array
    // (arr[l], ... arr[r]) Similar to as we do in binary
    // search
    let m = (l + r) / 2;

    // If these conditions follow that means Arr[m] is
    // binary searchable.
    if (LR < Arr[m] && Arr[m] < RL)
        ans = 1;

    // Finding the binary searchable elements to the left of
    // middle(m) element
    let l_ans = countBinarySearchableIndex(
        Arr, l, m - 1, LR, Math.min(RL, Arr[m]));

    // Finding the binary searchable elements to the right
    // of middle(m) element
    let r_ans = countBinarySearchableIndex(
        Arr, m + 1, r, Math.max(LR, Arr[m]), RL);

    return ans + l_ans + r_ans;
}

    let Arr = [ 10, 1,  2, 3, 4,  8,  6, 5,
                  7,  12, 9, 8, 13, 15, 11 ];
    let n = 15;
    console.log("Number of Binary Searchable Indexes: "+
    countBinarySearchableIndex(Arr, 0, n - 1, -1e9,
                                       1e9));

    // This code is contributed by poojaagarwal2.

Output

Number of Binary Searchable Indexes: 9

Time Complexity: O(n)
Auxiliary Space: O(log n) taken by Recursion Stack