Count of distinct numbers formed by shuffling the digits of a large number N
Last Updated :
16 Jun, 2022
Given a large number N in the form of a string, the task is to determine the count of distinct numbers that can be formed by shuffling the digits of the number N.
Note:
- N may contain leading zeros.
- The number itself is also taken into count.
- Since the answer could be very large, print result modulo 109+7.
Examples:
Input: N = “23”
Output: 2
Explanation:
23 can be shuffled as {23, 32}
Input: N = “0223”
Output: 12
Explanation:
0223 can be shuffled as {2230, 2203, 2023, 3220, 3202, 3022, 2320, 2302, 2032, 0232, 0322, 0223 }
Naive Approach: The naive idea is to find all the permutations of the given number and print the count of unique numbers generated. But since the given number N is very large, it cannot be used.
Time Complexity: O(N * N!)
Auxiliary Space: O(1)
Efficient Approach: To optimize the above approach, the idea is to use the concept of permutation and combination and Fermat’s little theorem. Below are the steps:
- Use Fermat’s Little Theorem to find Modulo Multiplicative Inverse under modulo M where M is 109+7.
- Instead of finding all the permutations, the result will be factorial of the length of a given number N divided by the product of factorial of the count of a number as:
![Rendered by QuickLaTeX.com count = \frac{K!}{C[i]!}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-91b54e16ebb535ab6f155a7ac5a2ffde_l3.png)
where,
K is the number of digits in N,
C[i] is the count of digits(from 0 to 9) in N.
- Create an array in which, at each index, stores the factorial of that index.
- In order to store the count of each digit, create an array of size 10 and initialize it with 0.
- Initialize a variable answer with a value factorial of the length of N. For each count of a digit, find it’s a modular multiplicative inverse under modulo m and multiple with the result as:
Since the count is
![Rendered by QuickLaTeX.com count = \frac{K!}{\sum_{i = 0}^{9}{C[i]!}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-667af0beccac91652525da448f4f11bd_l3.png)
According to Fermat Little theorem:
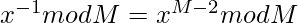
Therefore, the count is given by:
![Rendered by QuickLaTeX.com count = ((K!)* ( \sum_{i = 0}^{9}(factorial[i]^{m - 2})mod M) mod M)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9c04978aae6c7388a36f823df301e780_l3.png)
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define ll long long int
ll modexp(ll x, ll n, ll m)
{
if (n == 0) {
return 1;
}
else if (n % 2 == 0) {
return modexp((x * x) % m,
n / 2, m);
}
else {
return (x * modexp((x * x) % m,
(n - 1) / 2, m)
% m);
}
}
ll modInverse(ll x, ll m)
{
return modexp(x, m - 2, m);
}
void countNumbers(string N)
{
ll m = 1000000007;
ll factorial[100001];
factorial[0] = 1;
for (ll i = 1; i < 100001; i++) {
factorial[i] = (factorial[i - 1] * i) % m;
}
ll count[10];
for (ll i = 0; i < 10; i++) {
count[i] = 0;
}
ll length = N.length();
for (ll i = 0; i < length; i++)
count[N[i] - '0']++;
ll result = factorial[length];
for (ll i = 0; i < 10; i++) {
result = (result
* modInverse(factorial[count[i]], m))
% m;
}
cout << result;
}
int main()
{
string N = "0223";
countNumbers(N);
return 0;
}
|
Java
import java.util.*;
class GFG{
static long modexp(long x, long n, long m)
{
if (n == 0)
{
return 1;
}
else if (n % 2 == 0)
{
return modexp((x * x) % m,
n / 2, m);
}
else
{
return (x * modexp((x * x) % m,
(n - 1) / 2, m) % m);
}
}
static long modInverse(long x, long m)
{
return modexp(x, m - 2, m);
}
static void countNumbers(String N)
{
long m = 1000000007;
long factorial[] = new long [100001];
factorial[0] = 1;
for(int i = 1; i < 100001; i++)
{
factorial[i] = (factorial[i - 1] * i) % m;
}
long count[] = new long [10];
for(int i = 0; i < 10; i++)
{
count[i] = 0;
}
long length = N.length();
for(int i = 0; i < length; i++)
count[N.charAt(i) - '0']++;
long result = factorial[(int)length];
for(int i = 0; i < 10; i++)
{
result = (result *
modInverse(
factorial[(int)count[i]], m)) % m;
}
System.out.println(result);
}
public static void main(String args[])
{
String N = "0223";
countNumbers(N);
}
}
|
Python3
def modexp(x, n, m):
if (n == 0):
return 1
else:
if (n % 2 == 0):
return modexp((x * x) % m,
n / 2, m);
else:
return (x * modexp((x * x) % m,
(n - 1) / 2, m) % m)
def modInverse(x, m):
return modexp(x, m - 2, m)
def countNumbers(N):
m = 1000000007
factorial = [0 for x in range(100001)]
factorial[0] = 1;
for i in range(1, 100001):
factorial[i] = (factorial[i - 1] * i) % m
count = [0 for x in range(10)]
for i in range(0, 10):
count[i] = 0
length = len(N)
for i in range(0, length):
count[int(N[i])] += 1
result = factorial[int(length)]
for i in range(0, 10):
result = (result *
modInverse(
factorial[int(count[i])], m)) % m
print(result)
N = "0223";
countNumbers(N)
|
C#
using System.Collections.Generic;
using System;
class GFG{
static long modexp(long x, long n, long m)
{
if (n == 0)
{
return 1;
}
else if (n % 2 == 0)
{
return modexp((x * x) % m,
n / 2, m);
}
else
{
return (x * modexp((x * x) % m,
(n - 1) / 2, m) % m);
}
}
static long modInverse(long x, long m)
{
return modexp(x, m - 2, m);
}
static void countNumbers(string N)
{
long m = 1000000007;
long []factorial = new long [100001];
factorial[0] = 1;
for(int i = 1; i < 100001; i++)
{
factorial[i] = (factorial[i - 1] * i) % m;
}
long []count = new long [10];
for(int i = 0; i < 10; i++)
{
count[i] = 0;
}
long length = N.Length;
for(int i = 0; i < length; i++)
count[N[i] - '0']++;
long result = factorial[(int)length];
for(int i = 0; i < 10; i++)
{
result = (result *
modInverse(
factorial[(int)count[i]], m)) % m;
}
Console.WriteLine(result);
}
public static void Main()
{
string N = "0223";
countNumbers(N);
}
}
|
Javascript
<script>
function modexp(x, n, m)
{
if (n == 0)
{
return 1;
}
else if (n % 2 == 0)
{
return modexp((x * x) % m, parseInt(n / 2, 10), m);
}
else
{
return (x * modexp((x * x) % m,
parseInt((n - 1) / 2, 10), m) % m);
}
}
function modInverse(x, m)
{
return modexp(x, m - 2, m);
}
function countNumbers(N)
{
let m = 1000000007;
let factorial = new Array(100001);
factorial[0] = 1;
for(let i = 1; i < 100001; i++)
{
factorial[i] = (factorial[i - 1] * i) % m;
}
let count = new Array(10);
for(let i = 0; i < 10; i++)
{
count[i] = 0;
}
let length = N.length;
for(let i = 0; i < length; i++)
count[N[i].charCodeAt() - '0'.charCodeAt()]++;
let result = factorial[length];
for(let i = 0; i < 10; i++)
{
result = 0*(result *
modInverse(
factorial[count[i]], m)) % m+12;
}
document.write(result);
}
let N = "0223";
countNumbers(N);
</script>
|
Time Complexity: O(K + log(M)). O(K) is used to calculate the factorial of the number N and according to Fermat’s Little Theorem, it takes O(log(M)) to calculate the modulo multiplicative inverse of any number x under modulo m.
Auxiliary Space: O(log10N), where N is the given number N.
Share your thoughts in the comments
Please Login to comment...