Count of decrement operations required to obtain K in N steps
Last Updated :
17 May, 2021
Given two integers N and K, denoting the number of operations allowed and the number that needs to be obtained after performing N operations respectively. Consider a value S, initially 0, the task is to convert S to K by performing the following operations N times in any manner:
- Subtract 1 from S.
- Add P + 1 to S, where P is the number added previously(initially 0).
If it is not possible to convert S to K, print -1. Otherwise, print the number of decrement operations are required to be performed.
Note: S must be positive after every operation performed.
Examples:
Input: N = 5, K = 4
Output: 2
Explanation:
The order of the N operations performed:
Step 1: Adding 1 to S converts S = 1
Step 2: Adding 2 to S converts S = 3
Step 3: Subtracting 1 from S converts S = 2
Step 4: Adding 3 to S converts S = 5
Step 5: Subtracting 1 from S converts S = 4.
Since S is equal to K after N(= 5) operations, the answer is 2 as 2 decrement operations are performed.
Input: N = 10, K = 3
Output: -1
Naive Approach: The simplest idea is to iterate a loop over the range [1, N] and check for the following conditions:
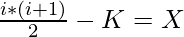
and i + K = N.
If there exists any value of i from the range [1, N] satisfying the above conditions, then print the value of i. Otherwise, print “-1”.
Time Complexity: O(N), where N is the maximum number of steps allowed.
Auxiliary Space: O(1)
Efficient Approach: To optimize the above approach, the idea is to use Binary Search. Below are the steps:
- Initialize two variables start as 0 and end as N.
- Find the middle index of the above two variables by taking the average of start and end.
- Check if we can have a mid number of steps of Type 1. If yes, then print mid and stop the iteration.
- Else update start or end according to the results we get by checking mid and repeat from step 2.
- If there doesn’t exist any mid satisfying the given condition then print “-1”.
Below is the implementation for the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int isValid(int n, int m, int k)
{
int step2 = n - m;
int cnt = (step2 * (step2 + 1)) / 2;
if (cnt - m == k)
return 0;
if (cnt - m > k)
return 1;
return -1;
}
void countOfOperations(int n, int k)
{
int start = 0, end = n;
bool ok = 1;
while (start <= end) {
int mid = (start + end) / 2;
int temp = isValid(n, mid, k);
if (temp == 0) {
ok = 0;
cout << mid;
break;
}
else if (temp == 1) {
start = mid + 1;
}
else {
end = mid - 1;
}
}
if (ok)
cout << "-1";
}
int main()
{
int N = 5, K = 4;
countOfOperations(N, K);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int isValid(int n, int m, int k)
{
int step2 = n - m;
int cnt = (step2 * (step2 + 1)) / 2;
if (cnt - m == k)
return 0;
if (cnt - m > k)
return 1;
return -1;
}
static void countOfOperations(int n, int k)
{
int start = 0, end = n;
boolean ok = true;
while (start <= end)
{
int mid = (start + end) / 2;
int temp = isValid(n, mid, k);
if (temp == 0)
{
ok = false;
System.out.print(mid);
break;
}
else if (temp == 1)
{
start = mid + 1;
}
else
{
end = mid - 1;
}
}
if (ok)
System.out.print("-1");
}
public static void main(String[] args)
{
int N = 5, K = 4;
countOfOperations(N, K);
}
}
|
Python3
def isValid(n, m, k):
step2 = n - m
cnt = (step2 * (step2 + 1)) // 2
if (cnt - m == k):
return 0
if (cnt - m > k):
return 1
return -1
def countOfOperations(n, k):
start = 0
end = n
ok = 1
while(start <= end):
mid = (start + end) // 2
temp = isValid(n, mid, k)
if (temp == 0):
ok = 0
print(mid)
break
elif (temp == 1):
start = mid + 1
else:
end = mid - 1
if (ok):
print("-1")
N = 5
K = 4
countOfOperations(N, K)
|
C#
using System;
class GFG{
static int isValid(int n,
int m, int k)
{
int step2 = n - m;
int cnt = (step2 *
(step2 + 1)) / 2;
if (cnt - m == k)
return 0;
if (cnt - m > k)
return 1;
return -1;
}
static void countOfOperations(int n,
int k)
{
int start = 0, end = n;
bool ok = true;
while (start <= end)
{
int mid = (start + end) / 2;
int temp = isValid(n, mid, k);
if (temp == 0)
{
ok = false;
Console.Write(mid);
break;
}
else if (temp == 1)
{
start = mid + 1;
}
else
{
end = mid - 1;
}
}
if (ok)
Console.Write("-1");
}
public static void Main(String[] args)
{
int N = 5, K = 4;
countOfOperations(N, K);
}
}
|
Javascript
<script>
function isValid(n, m, k)
{
var step2 = n - m;
var cnt = parseInt((step2 * (step2 + 1)) / 2);
if (cnt - m == k)
return 0;
if (cnt - m > k)
return 1;
return -1;
}
function countOfOperations(n, k)
{
var start = 0, end = n;
var ok = 1;
while (start <= end) {
var mid = parseInt((start + end) / 2);
var temp = isValid(n, mid, k);
if (temp == 0) {
ok = 0;
document.write( mid);
break;
}
else if (temp == 1) {
start = mid + 1;
}
else {
end = mid - 1;
}
}
if (ok)
document.write( "-1");
}
var N = 5, K = 4;
countOfOperations(N, K);
</script>
|
Time Complexity: O(log2N), where N is the given steps
Space Complexity: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...