Count of decreasing pairs formed from numbers 1 to N

Given an integer N, the task is to count of decreasing pairs from numbers 1 to N. 

A pair (x, y) is said to be decreasing if x > y

Examples:

Input: N = 8 
Output: 3 
Explanation:
Decreasing pairs are: (7, 1), (6, 2), (5, 3).
Input: N = 9 
Output: 4 
Explanation:
Decreasing pairs are: (8, 1), (7, 2), (6, 3), (5, 4). 

Approach: Consider the below cases:

If N = 1 => Count = 0 
If N = 2 => Count = 1 {(2, 1)} 
If N = 3 => Count = 1 {(3, 1) or (3, 2)} 
If N = 4 => Count = 2 {(4, 3), (2, 1)} 
If N = 5 => Count = 2 {(5, 4), (3, 2)} 
If N = 6 => Count = 3 {(6, 5), (4, 3), (2, 1)} 
. 
. 
and so on

It can be clearly observed that 

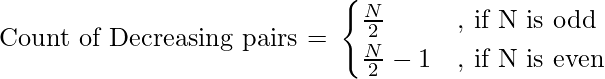
Below is the implementation of the above approach:

C++

// C++ program to count decreasing
// pairs formed from numbers 1 to N

#include <bits/stdc++.h>
using namespace std;

// Function to count the
// possible number of pairs
int divParts(int N)
{
    if (N % 2 == 0)

        // if the number is even
        // then the answer in (N/2)-1
        cout << (N / 2) - 1 << endl;

    else
        // if the number is odd
        // then the answer in N/2
        cout << N / 2 << endl;
}

// Driver code
int main()
{
    int N = 8;

    divParts(N);

    return 0;
}

Java

// Java program to count decreasing
// pairs formed from numbers 1 to N
import java.util.*;
class GFG{

// Function to count the
// possible number of pairs
static void divParts(int N)
{
    if (N % 2 == 0)

        // if the number is even
        // then the answer in (N/2)-1
        System.out.println((N / 2) - 1);

    else
        // if the number is odd
        // then the answer in N/2
        System.out.println((N / 2));
}

// Driver code
public static void main(String[] args)
{
    int N = 8;

    divParts(N);
}
}

// This code is contributed by offbeat

Python3

# Python3 program to count decreasing
# pairs formed from numbers 1 to N

# Function to count the
# possible number of pairs
def divParts(N):

    if (N % 2 == 0):

        # if the number is even
        # then the answer in (N/2)-1
        print((N / 2) - 1);

    else:

        # if the number is odd
        # then the answer in N/2
        print(N / 2);

# Driver code
N = 8;
divParts(N);

# This code is contributed by Code_Mech

C#

// C# program to count decreasing
// pairs formed from numbers 1 to N
using System;
class GFG{

// Function to count the
// possible number of pairs
static void divParts(int N)
{
    if (N % 2 == 0)

        // if the number is even
        // then the answer in (N/2)-1
        Console.WriteLine((N / 2) - 1);

    else
        // if the number is odd
        // then the answer in N/2
        Console.WriteLine((N / 2));
}

// Driver code
public static void Main()
{
    int N = 8;

    divParts(N);
}
}

// This code is contributed by Code_Mech

Javascript

<script>

// Javascript program to count decreasing
// pairs formed from numbers 1 to N

// Function to count the
// possible number of pairs
function divParts(N)
{
    if (N % 2 == 0)

        // if the number is even
        // then the answer in (N/2)-1
        document.write((N / 2) - 1);

    else
        // if the number is odd
        // then the answer in N/2
        document.write((N / 2));
}

// Driver Code

    let N = 8;

    divParts(N);

</script>

Output:

3

Time Complexity: O(1)

Space Complexity: O(1) as no extra space has been used.