Count of Binary strings of length N having atmost M consecutive 1s or 0s alternatively exactly K times
Last Updated :
07 Nov, 2023
Given three integers, N, K and M. The task is to find out the number of binary strings of length N which always starts with 1, in which there can be at most M consecutive 1’s or 0’s and they alternate exactly K times.
Examples:
Input: N = 5, K = 3, M = 2
Output: 3
The 3 configurations are:
11001
10011
11011
Explanation:
Notice that the groups of 1’s and 0’s alternate exactly K times
Input: N = 7, K = 4, M = 3
Output: 16
Approach: Since this problem involves both overlapping sub-problem and optimal substructure. So, this problem can be solved using dynamic programming.
- Sub-problem: DP[i][j] represents the number of binary strings upto length i having j alternating groups till now. So, to calculate dp[N][K] if we know the value of dp[n-j][k-1], then we can easily get the result by summing up the sub-problem value over j = 1 to m (DP[N][K] represents the final answer).
As shown below in the recursion tree diagram, it is observed many sub-problem overlaps. So, the result needs to be cached to avoid redundant calculations.
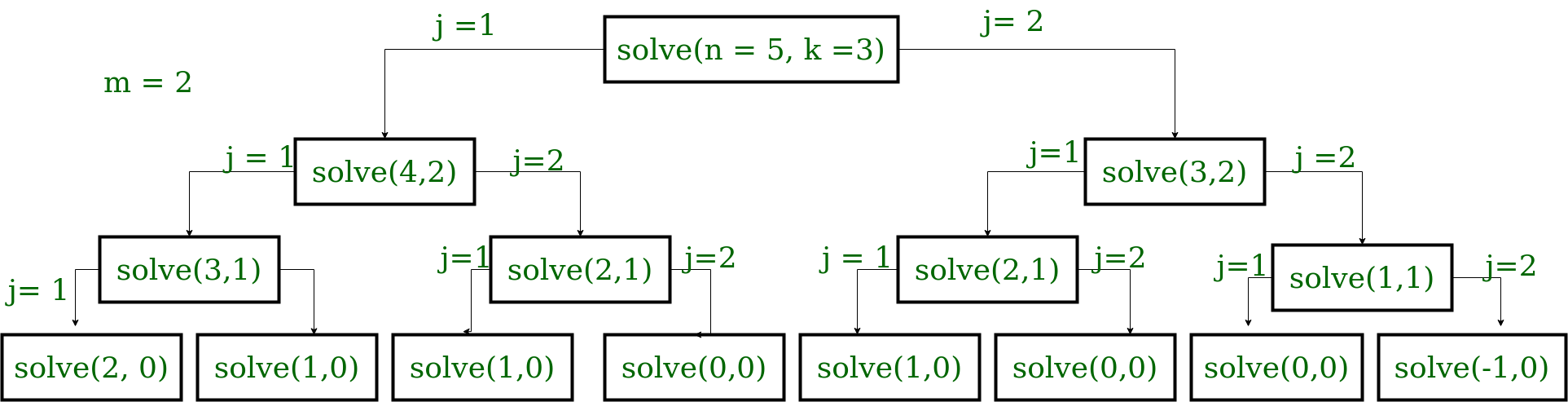
- Optimal substructure:
![Rendered by QuickLaTeX.com $dp[i][j]=$$\sum_{j=1}^{M} f(N-j, K-1)](https://quicklatex.com/cache3/36/ql_cb89348903685810c9bbe170f6cd7e36_l3.png)
- By following the top-down DP approach:
As we can have a group which can be atmost of the length M, so we iterate on every possible length and recur with new N and decreasing K by 1, as a new group is formed. Solution to sub-problem is cached and summed up to give final result dp[N][K].
- Base Case:
- When N is 0 and K is 0, then return 1
- When N is 0 but K is not 0, then return 0
- When N is not 0 but K is 0, then return 0
- When both are negative, return 0
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int dp[1000][1000];
int solve(int n, int k, int m)
{
if (n == 0 && k == 0)
return 1;
if (n == 0 && k != 0)
return 0;
if (n != 0 && k == 0)
return 0;
if (n < 0 || k < 0)
return 0;
if (dp[n][k])
return dp[n][k];
int ans = 0;
for (int j = 1; j <= m; j++) {
ans += solve(n - j, k - 1, m);
}
return dp[n][k] = ans;
}
int main()
{
int N = 7, K = 4, M = 3;
cout << solve(N, K, M);
}
|
Java
import java.util.*;
class GFG{
static int [][]dp = new int[1000][1000];
static int solve(int n, int k, int m)
{
if (n == 0 && k == 0)
return 1;
if (n == 0 && k != 0)
return 0;
if (n != 0 && k == 0)
return 0;
if (n < 0 || k < 0)
return 0;
if (dp[n][k] > 0)
return dp[n][k];
int ans = 0;
for(int j = 1; j <= m; j++)
{
ans += solve(n - j, k - 1, m);
}
return dp[n][k] = ans;
}
public static void main(String[] args)
{
int N = 7, K = 4, M = 3;
System.out.print(solve(N, K, M));
}
}
|
Python 3
rows, cols = (1000, 1000)
dp = [[0 for i in range(cols)]
for j in range(rows)]
def solve(n, k, m):
if n == 0 and k == 0:
return 1
if n == 0 and k != 0:
return 0
if n != 0 and k == 0:
return 0
if n < 0 or k < 0:
return 0
if dp[n][k]:
return dp[n][k]
ans = 0
for j in range(1, m + 1):
ans = ans + solve(n - j,
k - 1, m)
dp[n][k] = ans
return dp[n][k]
N = 7
K = 4
M = 3
print(solve(N, K, M))
|
C#
using System;
class GFG{
static int [,]dp = new int[1000, 1000];
static int solve(int n, int k, int m)
{
if (n == 0 && k == 0)
return 1;
if (n == 0 && k != 0)
return 0;
if (n != 0 && k == 0)
return 0;
if (n < 0 || k < 0)
return 0;
if (dp[n, k] > 0)
return dp[n, k];
int ans = 0;
for(int j = 1; j <= m; j++)
{
ans += solve(n - j, k - 1, m);
}
return dp[n, k] = ans;
}
public static void Main(String[] args)
{
int N = 7, K = 4, M = 3;
Console.Write(solve(N, K, M));
}
}
|
Javascript
<script>
dp = Array(1000);
for(i =0;i<1000;i++)
dp[i] = Array(1000).fill(0);
function solve(n , k , m)
{
if (n == 0 && k == 0)
return 1;
if (n == 0 && k != 0)
return 0;
if (n != 0 && k == 0){
return 0;
}
if (n < 0 || k < 0)
return 0;
if (dp[n][k] > 0)
return dp[n][k];
var ans = 0;
for (var j = 1; j <= m; j++) {
ans += solve(n - j, k - 1, m);
}
return dp[n][k] = ans;
}
var N = 7, K = 4, M = 3;
document.write(solve(N, K, M));
</script>
|
Time complexity: O(N*K*M)
Auxiliary Space: O(1000*1000)
Efficient approach : Using DP Tabulation method ( Iterative approach )
The approach to solve this problem is same but DP tabulation(bottom-up) method is better then Dp + memoization(top-down) because memoization method needs extra stack space of recursion calls.
Steps to solve this problem :
- Create a DP to store the solution of the subproblems and initialize it with 0.
- Initialize the DP with base cases dp[0][0] = 1.
- Now Iterate over subproblems to get the value of current problem form previous computation of subproblems stored in DP
- Return the final solution stored in dp[n][k].
Implementation :
C++
#include <bits/stdc++.h>
using namespace std;
int countBinaryStrings(int n, int k, int m) {
vector<vector<int>> dp(n + 1, vector<int>(k + 1, 0));
dp[0][0] = 1;
for (int i = 1; i <= m && i <= n; i++) {
dp[i][1] = 1;
}
for (int i = 1; i <= n; i++) {
for (int j = 2; j <= k; j++) {
for (int l = 1; l <= m && l <= i; l++) {
dp[i][j] += dp[i - l][j - 1];
}
}
}
return dp[n][k];
}
int main() {
int n = 7, k = 4, m = 3;
cout << countBinaryStrings(n, k, m) << endl;
return 0;
}
|
Java
import java.util.*;
public class Main {
static int countBinaryStrings(int n, int k, int m) {
int[][] dp = new int[n + 1][k + 1];
dp[0][0] = 1;
for (int i = 1; i <= m && i <= n; i++) {
dp[i][1] = 1;
}
for (int i = 1; i <= n; i++) {
for (int j = 2; j <= k; j++) {
for (int l = 1; l <= m && l <= i; l++) {
dp[i][j] += dp[i - l][j - 1];
}
}
}
return dp[n][k];
}
public static void main(String[] args) {
int n = 7, k = 4, m = 3;
System.out.println(countBinaryStrings(n, k, m));
}
}
|
Python3
def countBinaryStrings(n, k, m):
dp = [[0] * (k + 1) for i in range(n + 1)]
dp[0][0] = 1
for i in range(1, min(m+1, n+1)):
dp[i][1] = 1
for i in range(1, n+1):
for j in range(2, k+1):
for l in range(1, min(m+1, i+1)):
dp[i][j] += dp[i-l][j-1]
return dp[n][k]
n = 7
k = 4
m = 3
print(countBinaryStrings(n, k, m))
|
C#
using System;
class Program
{
static int CountBinaryStrings(int n, int k, int m)
{
int[,] dp = new int[n + 1, k + 1];
dp[0, 0] = 1;
for (int i = 1; i <= m && i <= n; i++)
{
dp[i, 1] = 1;
}
for (int i = 1; i <= n; i++)
{
for (int j = 2; j <= k; j++)
{
for (int l = 1; l <= m && l <= i; l++)
{
dp[i, j] += dp[i - l, j - 1];
}
}
}
return dp[n, k];
}
static void Main()
{
int n = 7, k = 4, m = 3;
Console.WriteLine(CountBinaryStrings(n, k, m));
}
}
|
Javascript
function countBinaryStrings(n, k, m) {
const dp = new Array(n + 1);
for (let i = 0; i <= n; i++) {
dp[i] = new Array(k + 1).fill(0);
}
dp[0][0] = 1;
for (let i = 1; i <= m && i <= n; i++) {
dp[i][1] = 1;
}
for (let i = 1; i <= n; i++) {
for (let j = 2; j <= k; j++) {
for (let l = 1; l <= m && l <= i; l++) {
dp[i][j] += dp[i - l][j - 1];
}
}
}
return dp[n][k];
}
const n = 7;
const k = 4;
const m = 3;
console.log(countBinaryStrings(n, k, m));
|
Time complexity: O(N*K*M)
Auxiliary Space: O(N*K)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...